filmov
tv
Olympiad Geometry Problem #41: Mixtilinear Incircles

Показать описание
Here is a very useful configuration in many geometry problems, even those which don't explicitly state that they involve mixtilinear incircles. I'm following the exposition from a free ebook called A Beautiful Journey in Olympiad Geometry (which has a suggested donation). Enjoy!
Olympiad Geometry Problem #41: Mixtilinear Incircles
Olympiad Geometry Problem #81: Altitude, Two Circles, Concurrence
Element 101. The Mixtilinear Incircles and Excircles | Elements in Geometry for Olympiads
Olympiad Geometry Problem #70: Cyclic Quad, Equal Segements, Perpendicuar
Olympiad Geometry Problem #100: Circumcenter Perpendiculars Cyclic Quad
Olympiad Geometry Problem #71: Isogonal Line Lemma
Olympiad Geometry Problem #40: IMO Shortlist 2003 G4 - Four Circles
Olympiad Geometry Problem #105: USA AIME #15 - Solved Two Different Ways!
Olympiad Geometry Problem #48: Gauss Line
LIVESTREAM GEO #51A: A Hard Mixtilinear Problem, and an Interesting Tangency Problem
Olympiad Geometry Problem #39: Circumcenter, Incenter, Double Segment
Olympiad Geometry Problem #18: Altitudes, Circumcircle, Equal Segments
Olympiad Geometry Problem #42: Isosceles Triangle, Median, Altitude, Midpoint
Olympiad Geometry Problem #78: Incenter, Midpoint, Parallel
LIVESTREAM GEO #82B: Triple Mixtilinear Incircles and an Orthocenter!
Mixlinear Circle
Olympiad Geometry Problem #35: Angle Bisector, Perpendiculars, Tangency
Olympiad Geometry Problem #89: Reflections, Tangents, Perpendicular
Olympiad Geometry Problem #16: 60 Degrees, Bisector, Reflection
Olympiad Geometry Problem #24: Perpendiculars, Circumcircles, Concurrence
A problem from Moscow Math Olympiad 1941
A geometry problem about 3 circles from New Zealand Mathematical Olympiad, 2021, round 2
Olympiad Geometry Problem #74: Incircle, Equal Segments, Right Angle
Prove 3 Points Are Collinear: A Geometry Problem from 2021 China's Math Olympiad
Комментарии
 0:15:24
0:15:24
 0:15:23
0:15:23
 0:11:43
0:11:43
 0:11:22
0:11:22
 0:07:54
0:07:54
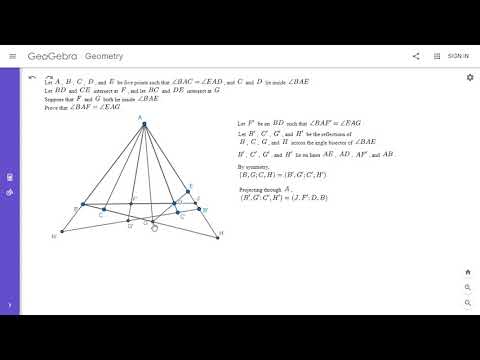 0:11:42
0:11:42
 0:12:12
0:12:12
 0:17:04
0:17:04
 0:16:00
0:16:00
 1:37:23
1:37:23
 0:10:13
0:10:13
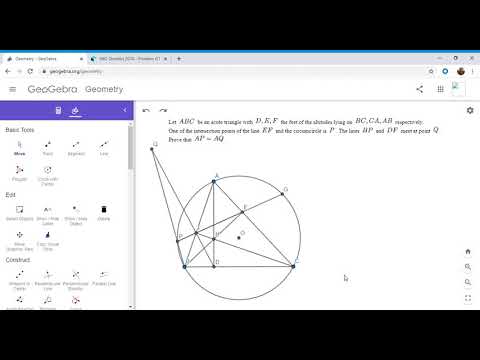 0:12:18
0:12:18
 0:13:46
0:13:46
 0:08:17
0:08:17
 1:35:05
1:35:05
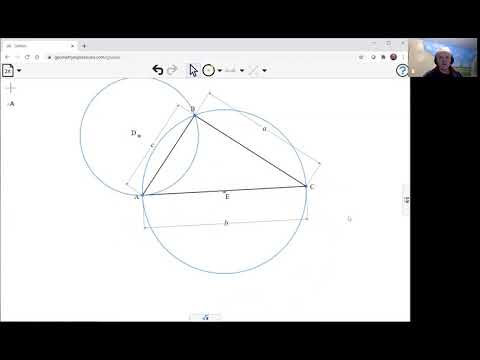 0:03:20
0:03:20
 0:10:33
0:10:33
 0:22:52
0:22:52
 0:11:08
0:11:08
 0:06:53
0:06:53
 0:03:12
0:03:12
 0:12:34
0:12:34
 0:17:04
0:17:04
 0:14:52
0:14:52