Residue calculus integration example with simple poles, Complex Analysis

Показать описание

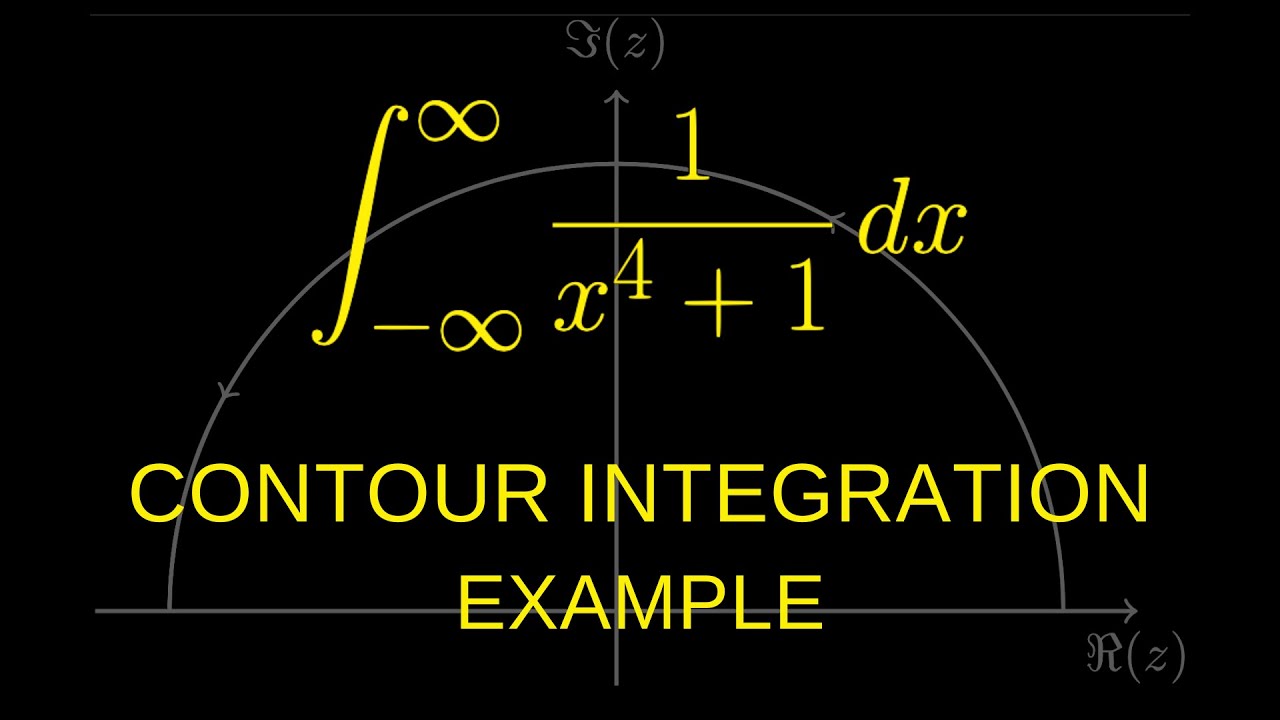
In greater detail, I start by extending the function into the complex plane as f(z)=1/(z^4+1), note that the degree of the denominator is at least two greater than the numerator. Next, I identify the singularities of the function, which are the roots of z^4=-1, finding four distinct solutions that lie on the circle |z|=1 in the complex plane.

To evaluate the integral, I construct a contour in the upper half of the complex plane that encloses two of the four singularities so that we can use Cauchy's residue theorem to compute the integral around this contour. I then compute the residues at the enclosed singularities, simplifying the complex expressions involved. Finally, I demonstrate how the integral over the real line can be obtained by considering the limit of the contour integral as the radius of the semicircular part goes to infinity, subtracting the contribution from the semicircular path, which tends to zero. The final result of the integral is derived by summing the computed residues and applying Cauchy's residue theorem.

#complexanalysis #mathematics #Contourintegration #integration #CauchysResidueTheorem #residuecalculus #mathtutorial ##ResidueComputation