filmov
tv
Math Olympiad Problem | A Nice Algebra Challenge | You Should Know This Trick
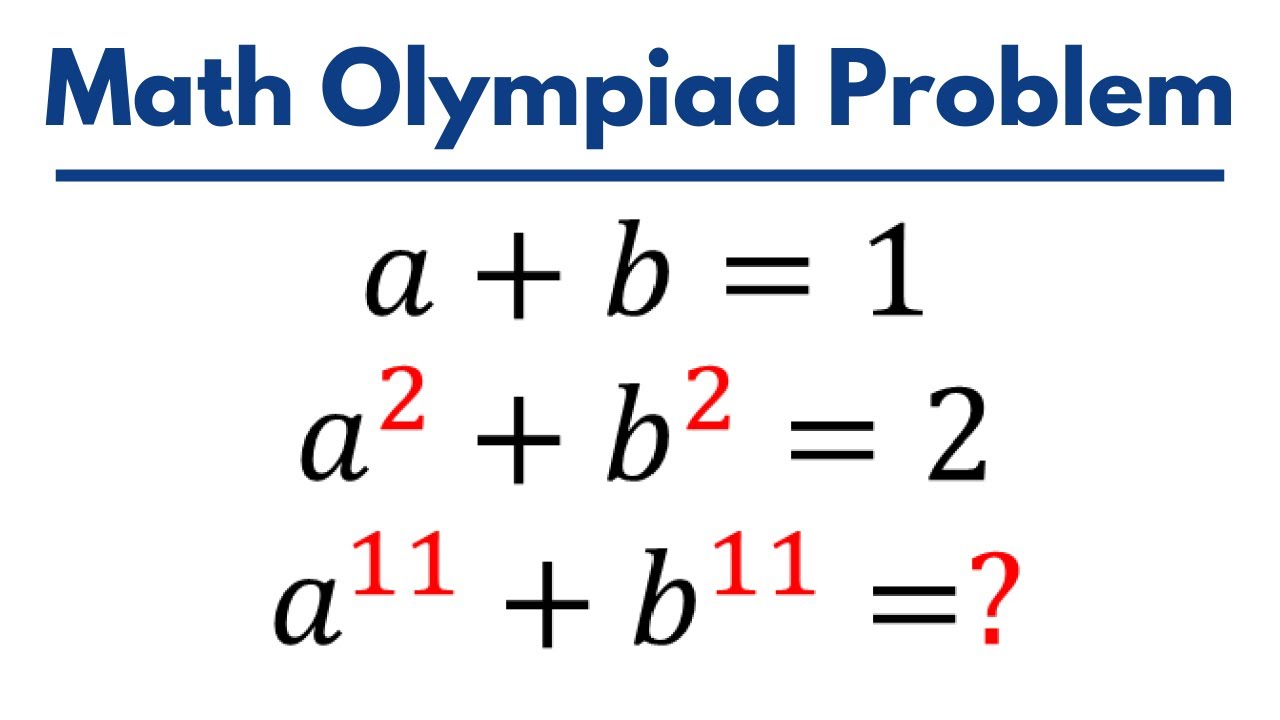
Показать описание
In this video, I am presenting step-by-step solutions to this interesting and nice algebra problem. This is an algebra problem that you need to analyze polynomial equation, working on quadratic equation and quartic equation at the same time to come up with the answer. This video will walk you through how to analyze polynomial equation or algebraic equation, working with exponential operation to come up with the final answer. This is a good practice for math olympiad, too. Come check this video out and watch it until the end. More to come! Stay tuned!
💬 Did you enjoy this video? Tell me all about it in the comment section below!
Subscribe to Dr. PK Math here ⤵️
*************
✅ Follow Modern Dr PK Math on social media:
*************
#DrPKMath #algebra #matholympiad
💬 Did you enjoy this video? Tell me all about it in the comment section below!
Subscribe to Dr. PK Math here ⤵️
*************
✅ Follow Modern Dr PK Math on social media:
*************
#DrPKMath #algebra #matholympiad
A beautiful international math olympiad problem
Germany - Math Olympiad Problem | Be Careful!
Many students failed to solve this Japan Math Olympiad Geometry Problem
Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1
The unexpectedly hard windmill question (2011 IMO, Q2)
Norway Math Olympiad Question | You should be able to solve this!
Solving the hardest question of a British Mathematical Olympiad
Mexico - A Nice Math Olympiad Exponential Problem
IOQM 2024 Problem 13 | Solution and Discussion | Math Olympiad in India
The Legend of Question Six - Numberphile
Iceland Math Olympiad Problem
Korean -Math Olympiad problem|Solve for x#matholympiad#math
You, me, and my first International Math Olympiad problem
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Regional Math Olympiad Problem
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Japanese Math Olympiad Problem | A Nice Math Problem : Comparison
Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988
Solving An Insanely Hard Problem For High School Students
A Nice Math Olympiad Exponential Equation 3^x = X^9
Challenging Math Olympiad Problem | Geometry Question | Mathematics | 2 Methods
Luxembourg - Math Olympiad Question | You should know this trick
Russia | Math Olympiad Question | You should know this trick!!
This U.S. Olympiad Coach Has a Unique Approach to Math
Комментарии
 0:01:00
0:01:00
 0:10:06
0:10:06
 0:09:27
0:09:27
 0:06:40
0:06:40
 0:16:03
0:16:03
 0:03:21
0:03:21
 0:11:26
0:11:26
 0:08:36
0:08:36
 0:07:38
0:07:38
 0:08:45
0:08:45
 0:02:54
0:02:54
 0:07:36
0:07:36
 0:31:21
0:31:21
 0:01:54
0:01:54
 0:13:55
0:13:55
 0:08:40
0:08:40
 0:04:15
0:04:15
 0:08:03
0:08:03
 0:07:27
0:07:27
 0:02:34
0:02:34
 0:25:44
0:25:44
 0:02:51
0:02:51
 0:08:01
0:08:01
 0:03:20
0:03:20