filmov
tv
Indian Mathematical Olympiad | 1992 Question 8

Показать описание
We present a solution to question 8 form the 1992 Indian Mathematical Olympiad. The goal of this question is to classify all perfect squares of the form 2^m+3^n.
Indian Mathematical Olympiad | 1992 Question 8
02 - International Math Olympiad 1992 P2
International Mathematical Olympiad, 1992, problem 2 (proposed by India)
Indian Mathematical Olympiad | 1992 Question 8
Solving an IMO Problem in 10 Minutes!! | International Mathematical Olympiad 1992 Problem 1
flanders Mathematical olympiad 1992
IMO 1992 Problem 2 | My elegant solution to this Functional equation problem
indian Mathematical olympiad
Math Olympiad for India and USA
Top 20 Country by International Mathematical Olympiad Gold Medal (1959-2019)
hard arithmetic indian Mathematical olympiad
indian mathematical Olympiad | find the value of a^8 + b^8 #algebra #olympiad #india #imo
India National Mathematical Olympiad 2017 Problem 6
hard arithmetic indian Mathematical olympiad
INDIA Mathematical Olympiad | SCHOOL OF OLYMPIAD | x & y Equation (L-7)
1992 IMO Problem #3
Two Ways to Solve a National Maths Olympiad Problem | India National MO 1990
The Answer is Surprisingly Easy! | India National Mathematics Olympiad 2003
IOQM|Diophantine equation|Math Olympiad
Find Natural Numbers A and B | Number Theory | Junior Math Olympiad Training
Prime Powers | India National Mathematical Olympiad 2008 Problem 2
Indian Mathematical Olympiad | RMO 2001
A Nice and Simple Equation in National Maths Olympiad
Indian Mathematical Olympiad | RMO 2016 | Tips & Tricks for RMO
Комментарии
 0:22:03
0:22:03
 0:16:32
0:16:32
 0:19:13
0:19:13
 0:28:09
0:28:09
 0:10:33
0:10:33
 0:12:13
0:12:13
 0:13:06
0:13:06
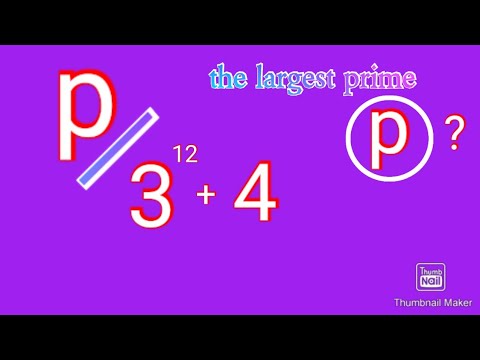 0:09:11
0:09:11
 0:00:35
0:00:35
 0:02:21
0:02:21
 0:11:54
0:11:54
 0:04:19
0:04:19
 0:16:24
0:16:24
 0:19:22
0:19:22
 0:05:21
0:05:21
 0:15:29
0:15:29
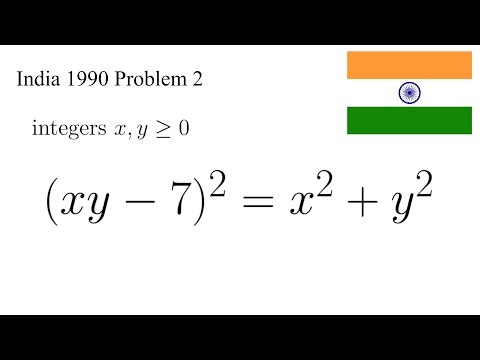 0:14:26
0:14:26
 0:06:47
0:06:47
 1:09:31
1:09:31
 0:03:04
0:03:04
 0:07:26
0:07:26
 0:07:28
0:07:28
 0:07:41
0:07:41
 0:08:33
0:08:33