filmov
tv
The Answer is Surprisingly Easy! | India National Mathematics Olympiad 2003
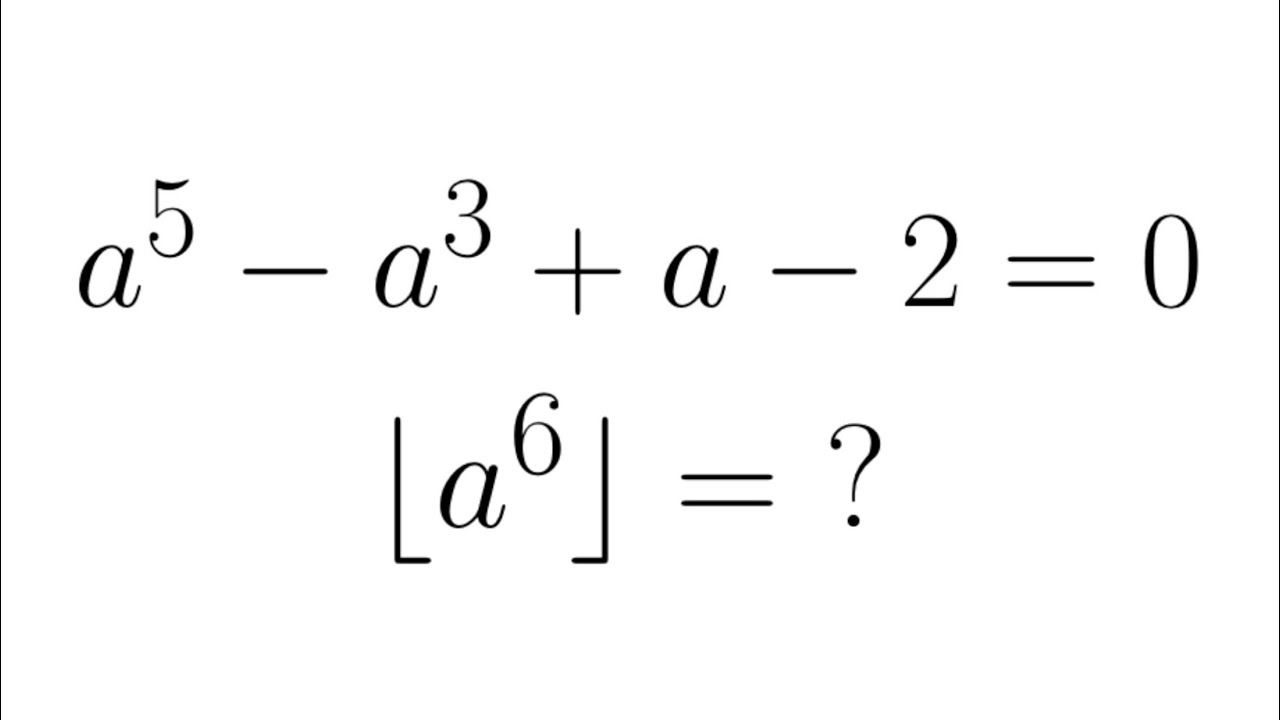
Показать описание
Surprisingly Easy Answer to the Apparent Paradox that Plagues Many Spiritual Seekers Today
Go is Surprisingly Easy
Mom freaks on Daughter for ordering Temu SHOCK KITTEN SURPRISE #viral #temu #kitty
Recreating CIA Technology Was Surprisingly Easy (Microdots)
The hardest test had this 'easy' question with a surprising answer
The answer is surprising and strangely satisfying - Euler's constant e appears from nowhere!
It's Surprisingly EASY to Kill an Old Person.
always catching mom by surprise #funny #greatness #dance
Unwrapping the Surprising Origins of Christmas Traditions
A Surprising Answer!
Going Under in Worlds Largest Toilet SURPRISE EGG Pool #shorts
She Gets A SURPRISE! 😱
ALIYAH MEETS TAYLOR SWIFT 😜 #surprise #aussiefamily #taylorswift #swiftie #meetingtaylorswift
The only networking advice you’ll ever need (it’s surprisingly simple)!
Her Birthday Surprise!😂
Trump's Surprising Answer to Question About His Age | NowThis
Surprising my husband with Ronaldo as a birthday gift 🎁 🥳
Teacher gets an incredible surprise during her class 🥹
Surprising Life Advice from an 18 Year Old
The answers are so surprising you won't believe them, even after seeing the calculations
Magnus Carlsen’s Surprise Opening 💀🔥 #magnuscarlsen #chess
Trading Common Pokemon Cards for RARE GOLD Cards! (Surprising Kids) #pokemon #surprise #reaction
90% fail : The Easiest Puzzle in the world || Longest Bridge || Surprising Answer
6 Impossible Puzzles With Surprising Solutions
Комментарии
 0:15:34
0:15:34
 0:09:57
0:09:57
 0:00:49
0:00:49
 0:17:26
0:17:26
 0:07:22
0:07:22
 0:05:30
0:05:30
 0:03:36
0:03:36
 0:00:16
0:00:16
 0:17:01
0:17:01
 0:02:23
0:02:23
 0:00:39
0:00:39
 0:00:23
0:00:23
 0:00:39
0:00:39
 0:00:51
0:00:51
 0:00:12
0:00:12
 0:00:31
0:00:31
 0:00:18
0:00:18
 0:00:16
0:00:16
 0:00:54
0:00:54
 0:09:29
0:09:29
 0:00:29
0:00:29
 0:00:26
0:00:26
 0:03:58
0:03:58
 0:12:46
0:12:46