filmov
tv
Trig Identity: Tan(x) = sin(2x) / [ cos(2x) + 1 ]

Показать описание
How I discovered a trig identity that I was not previously aware of using COMPLEX numbers and the Euler Identity:
exp(ix) = cos(x) + i sin(x)
The trig identity: Tan(x) = sin(2x) / [ cos(2x) + 1 ]
exp(ix) = cos(x) + i sin(x)
The trig identity: Tan(x) = sin(2x) / [ cos(2x) + 1 ]
Trig Identity: Tan(x) = sin(2x) / [ cos(2x) + 1 ]
Trig Identity tan x sin x/( tanx + sinx)
when calculus students use trig identities too early
How to Write Double Angle Formula sin 2x in terms of tan x
Trig Identity tan x/(1 + tan^2 x) = (sec x - cos x)(csc x - sin x) Proved from Both Sides
Proving Trig Identity tan(x) = sin(x)/cos(x) | A-Level Maths
Trigonometric Rational Identity Sin2x and Cos2x and tanx Q14
Trigonometry Identity: tan(-x) = -tan(x)
Trigonometric Identity (sinx + sin2x)/(1 + cosx + cos2x) = tanx with Double Angle Expressions
Proof sin2x=2sinxcosx
Prove trig identity (secx sinx)/(tanx +cotx) = sin^2x
Trigonometry | Show that cot(x) + tan(x) = 2/sin(2x)
Learn How To Prove A Trigonometry Question & Apply Trig Identities Effectively
#Trigonometry all formulas
24. Prove the Identity: tan^2x-sin^2x = tan^2x sin^2x
Verify Trig Identity sec x - cos x = sin x tan x. Common denominator
Prove that sin2x=2tanx/1+tan^2x
Trigonometry Identity: tan^2(x) + 1 = sec^2(x)
Trig Identities
Trigonometric Identity Tan To Tangent
Verifying a Trigonometric Identity tan(x)/sec(x) = sin(x)
Trigonometric Identity tan x + 1 = (cos^2x - sin^2x)/(cos^2x - sin x cos x) of Compound Angle
Visualizing the derivative of sin(x)
PreCalculus - Trigonometry: Trig Identities (34 of 57) Proof Half Angle Formula: tan(x/2)
Комментарии
 0:08:21
0:08:21
 0:00:43
0:00:43
 0:03:47
0:03:47
 0:05:18
0:05:18
 0:02:08
0:02:08
 0:04:14
0:04:14
 0:05:05
0:05:05
 0:03:19
0:03:19
 0:02:03
0:02:03
 0:01:28
0:01:28
 0:05:18
0:05:18
 0:13:17
0:13:17
 0:00:16
0:00:16
 0:01:43
0:01:43
 0:02:29
0:02:29
 0:02:39
0:02:39
 0:02:56
0:02:56
 0:27:57
0:27:57
 0:02:06
0:02:06
 0:01:07
0:01:07
 0:03:27
0:03:27
 0:00:59
0:00:59
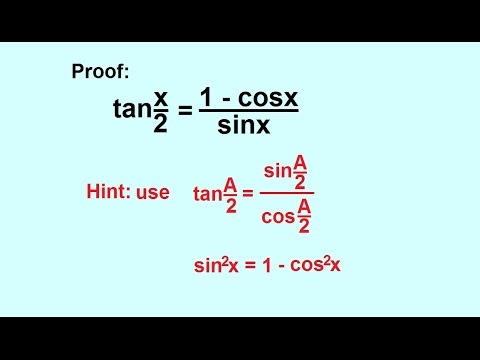 0:03:45
0:03:45