filmov
tv
Fundamental Solution of the Diffusion Equation using the Similarity Method

Показать описание
Explains the derivation of the Fundamental solution of the diffusion equation, also known as heat equation, using the similarity solutions method, which you might know as the group theoretical methods of Lie.
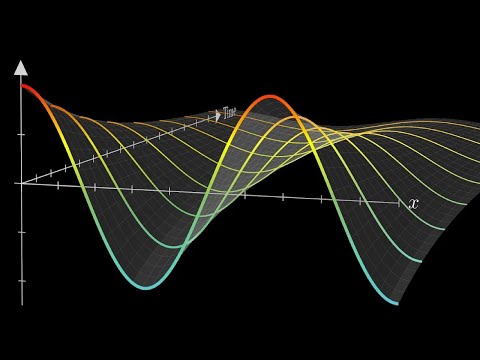
Fundamental Solution of the Diffusion Equation using the Similarity Method
Lecture 8: Solving the diffusion equation on the real line
Lecture 8: Properties of solutions to the diffusion equation
Lecture 9: Solving the diffusion equation on the real line
Solution of Diffusion-Convection Equation
Fundamental solution
Large-time asymptotics of fundamental solutions for diffusion equations in periodic media
Fundamental solution to the heat equation
Solving the heat equation | DE3
Fundamental solution set and wronskian
Fundamental solutions
Diffusion processes. Lecture 14. Portenko N.I.
Diffusion processes. Lecture 9. Portenko N.I.
Heat Equation
Diffusion processes. Lecture 15. Portenko N.I.
Diffusion processes. Lecture 5. Portenko N. I.
Diffusion processes. Lecture 12. Portenko N. I.
Lecture 6.2: Laplace equation - Fundamental solution
Lecture 7: Properties of the diffusion equation
Mod-10 Lec-25 The diffusion equation (Part I)
The Story of the Telegrapher's Equations - from diffusion to a wave.
Difference equations, Fundamental solutions, Part I
Mod-10 Lec-26 The diffusion equation (Part II)
Heat equation
Комментарии
 0:21:53
0:21:53
 0:59:29
0:59:29
 1:17:16
1:17:16
 0:59:29
0:59:29
 0:06:31
0:06:31
 0:26:11
0:26:11
 0:27:49
0:27:49
 0:00:29
0:00:29
 0:14:13
0:14:13
 0:06:16
0:06:16
 0:32:50
0:32:50
 1:34:22
1:34:22
 1:20:40
1:20:40
 0:21:19
0:21:19
 1:29:21
1:29:21
 1:28:53
1:28:53
 1:23:41
1:23:41
 0:27:21
0:27:21
 1:17:15
1:17:15
 0:44:26
0:44:26
 0:15:01
0:15:01
 0:11:47
0:11:47
 0:51:28
0:51:28
 0:32:41
0:32:41