filmov
tv
Heat Equation

Показать описание
Fundamental Solution of the Heat Equation
In this video, I derive the fundamental solution of the heat equation u_t = k u_xx by assuming the solution has a special form, and therefore turning the PDE into an ODE, which has an explicit solution. Enjoy!
In this video, I derive the fundamental solution of the heat equation u_t = k u_xx by assuming the solution has a special form, and therefore turning the PDE into an ODE, which has an explicit solution. Enjoy!
Solving the heat equation | DE3
Heat Equation
Oxford Calculus: How to Solve the Heat Equation
Deriving the Heat Equation: A Parabolic Partial Differential Equation for Heat Energy Conservation
But what is a partial differential equation? | DE2
Understanding Conduction and the Heat Equation
12.3: Heat Equation
PDE | Heat equation: intuition
The Heat Equation: Lecture 1 - Oxford Mathematics 1st Year Student Lecture
The Heat Equation + Special Announcement! | Infinite Series
PDE: Heat Equation - Separation of Variables
Heat equation: Separation of variables
Solving the Heat Equation with the Fourier Transform
Heat Equation
The Heat Equation and the Steady State Heat Distribution via Laplace's Equation
Solved Examples of Heat Equation | Part 1 | Easiest Way
Oxford Calculus: Heat Equation Derivation
Solution to the Heat Equation | Method of separation of variables
Deriving the Heat Equation in 2D & 3D (& in N Dimensions!) with Control Volumes and Vector C...
Solving PDEs with the Laplace Transform: The Heat Equation
Heat Equation | Separation of Variables Method in PDE | Example & Concepts by GP Sir
The diffusion equation | Week 12 | MIT 18.S191 Fall 2020 | Grant Sanderson
Specific Heat Equation Stated Clearly
Separation of Variables - Heat Equation Part 1
Комментарии
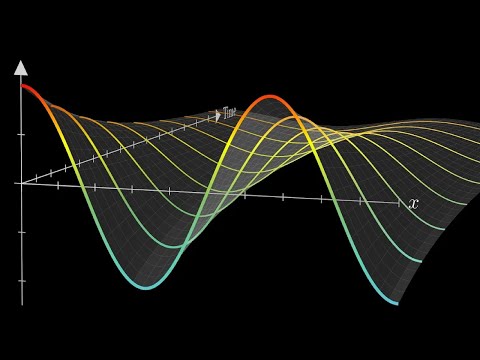 0:14:13
0:14:13
 0:10:48
0:10:48
 0:35:02
0:35:02
 0:23:50
0:23:50
 0:17:39
0:17:39
 0:18:21
0:18:21
 0:32:45
0:32:45
 0:07:56
0:07:56
 0:23:56
0:23:56
 0:11:27
0:11:27
 0:21:17
0:21:17
 0:47:14
0:47:14
 0:11:28
0:11:28
 0:21:19
0:21:19
 0:19:54
0:19:54
 0:39:38
0:39:38
 0:25:20
0:25:20
 0:36:48
0:36:48
 0:24:40
0:24:40
 0:40:16
0:40:16
 0:19:37
0:19:37
 0:21:30
0:21:30
 0:03:56
0:03:56
 0:09:01
0:09:01