filmov
tv
Integral using trig identities and IBP
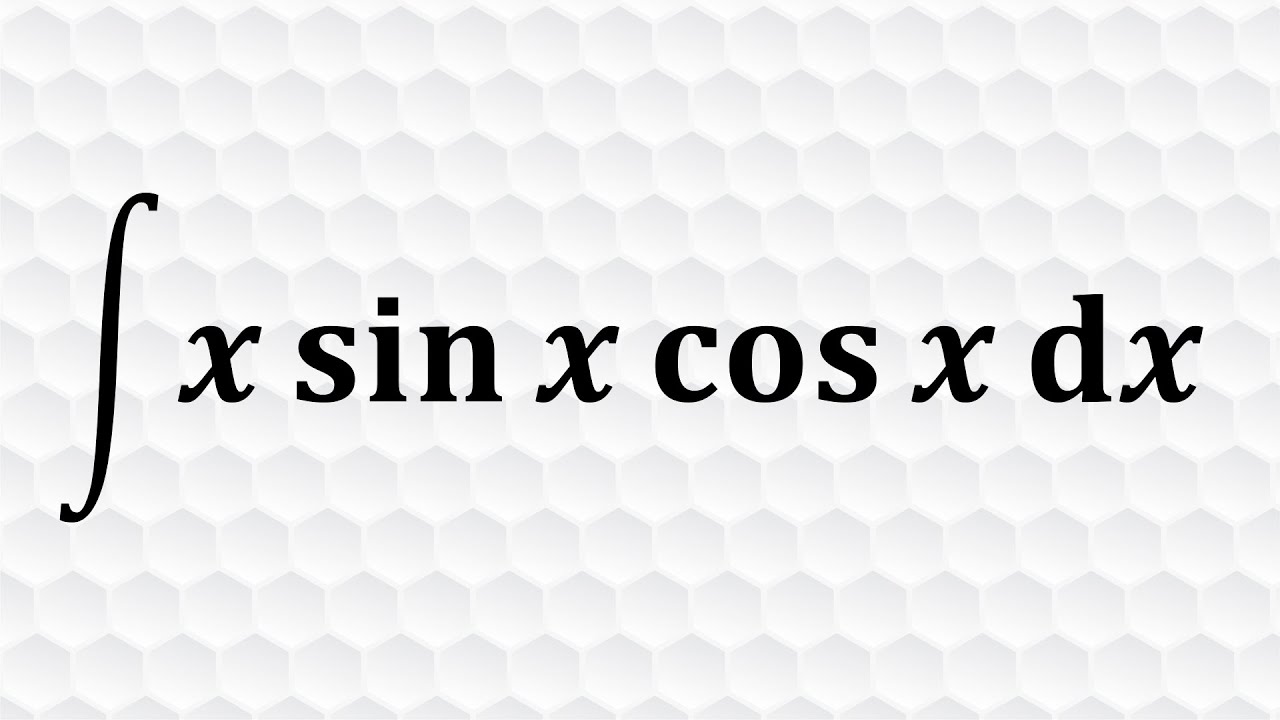
Показать описание
In this video, I showed how to modify and evaluate an integral using trig identities and IBP
Trigonometric Integrals
Evaluating Integrals With Trigonometric Functions
Integral using trig identities and IBP
when calculus students use trig identities too early
Integral using trig identities and U-sub
Trigonometric Substitution
Using trig identities for integration
Integration using Trig Identities
Integration By Trigonometric Identities l Integration-Part 3 l Math Madness By Aisha Khalid
Integration By Trigonometric Substitution
trig integrals involving sine and cosine (calculus 2)
Edexcel A level Maths: 11.3 Using Trigonometric Identities To Integrate
Trig identities for trig integral
Integration by Substitution involving Trigonometric ratios (Sine, Cosine and Tangent)
How to Do Integration With Trigonometry #shorts
Basic Trigonometric Substitution #shorts
Calculus 2 Lecture 7.2: Techniques For Trigonometric Integrals
Using angle sum identities for Integration
Integration using Trigonometric Identities | Integrals Class 12 | Class 12 Maths Chapter 7 | NCERT
Calculus 2 Lecture 7.3: Integrals By Trigonometric Substitution
Integration using trigonometric identities (3) | ExamSolutions
Integrate to make trig identities.
Trick for Memorizing Trig Integrals
PLUS TWO MATHEMATICS//INTEGRALS//EPISODE -6//TYPE5 /INTEGRATION USING TRIGONOMETRIC IDENTITIES
Комментарии
 0:31:29
0:31:29
 0:07:32
0:07:32
 0:10:53
0:10:53
 0:00:43
0:00:43
 0:07:51
0:07:51
 0:19:50
0:19:50
 0:07:15
0:07:15
 0:06:26
0:06:26
 0:13:44
0:13:44
 0:15:55
0:15:55
 0:15:42
0:15:42
 0:11:31
0:11:31
 0:05:32
0:05:32
 0:27:29
0:27:29
 0:00:26
0:00:26
 0:00:39
0:00:39
 2:21:10
2:21:10
 0:08:12
0:08:12
 0:21:01
0:21:01
 2:09:24
2:09:24
 0:05:14
0:05:14
 0:00:34
0:00:34
 0:07:17
0:07:17
 0:25:29
0:25:29