filmov
tv
Proof: Square Root of 3 is Irrational

Показать описание
We prove the square root of 3 is irrational. Proving some numbers are irrational is a real pain, but it doesn't always have to be so hard! To prove sqrt(3) is irrational, we can use the proof by contradiction strategy famously used to prove the square root of 2 is irrational. We'll assume that the square root of 3 is NOT irrational, and thus is rational. Then we'll write it as a ratio of integers in fully reduced form, and find a contradiction!
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Lyndon for their generous support on Patreon!
Follow Wrath of Math on...
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Lyndon for their generous support on Patreon!
Follow Wrath of Math on...
Proof: Square Root of 3 is Irrational
🔶03 - Show that Square Root of 3 is irrational | Square Root of all Prime Numbers are Irrational
Proof that the square root of 3 is irrational
A-Level Maths: A1-12 Proving √3 is Irrational
Proof that √3 (square root of 3) is irrational by contradiction
Proof: √3 + √2 is irrational
Prove that sqrt(2) + sqrt(3) Cannot be a Rational Number
Proof that the square root of ANY integer is irrational (besides perfect squares)
Maths 2 | TA Session - Week 1b
Visual irrationality proofs from the carpets theorem (root 2 and root 3)
A Proof That The Square Root of Two Is Irrational
Proof that square root of prime number is irrational | Algebra I | Khan Academy
Proof: Square Root of 2 is Irrational
Prove Root 2 / Root 3 / Root 5 Irrational? in 9 mins | Revision for Class 10th MATHS Board Exam 🎯
A-Level Maths: A1-13 Proving √3 is Irrational - Alternative Method
How to Find Value of Irrational Numbers correct to three decimal places Square root 2 without calcul
Prove that sqrt(2) + sqrt(3) is irrational [ILIEKMATHPHYSICS]
Prove that root2+root3 is irrational-Real numbers-Class10
Prove that √3 is irrational.
Trick 254 - Proving that Square Root of 3 is Irrational
Irrational Root 2!
06-Prove Square Root 3 is Irrational. Class 11th Example 3 chap1. Algebra and trigonometry.
Cubed Root Of 2 Is Irrational
Proving Square Root of 3 is Irrational | Math Dot Com
Комментарии
 0:06:13
0:06:13
 0:10:09
0:10:09
 0:08:12
0:08:12
 0:05:21
0:05:21
 0:02:54
0:02:54
 0:18:57
0:18:57
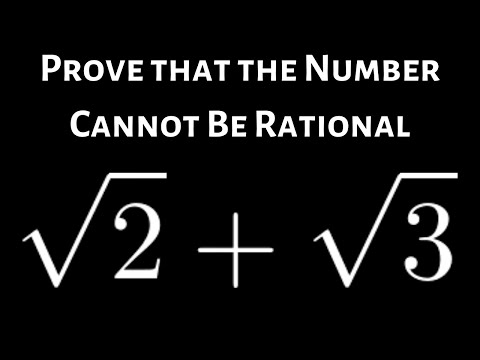 0:05:34
0:05:34
 0:06:00
0:06:00
 3:19:33
3:19:33
 0:04:40
0:04:40
 0:17:22
0:17:22
 0:07:28
0:07:28
 0:04:02
0:04:02
 0:09:03
0:09:03
 0:08:58
0:08:58
 0:08:35
0:08:35
 0:03:51
0:03:51
 0:02:09
0:02:09
 0:08:42
0:08:42
 0:07:19
0:07:19
 0:00:59
0:00:59
 0:06:32
0:06:32
 0:00:36
0:00:36
 0:06:08
0:06:08