filmov
tv
This Integral Will Surprise You
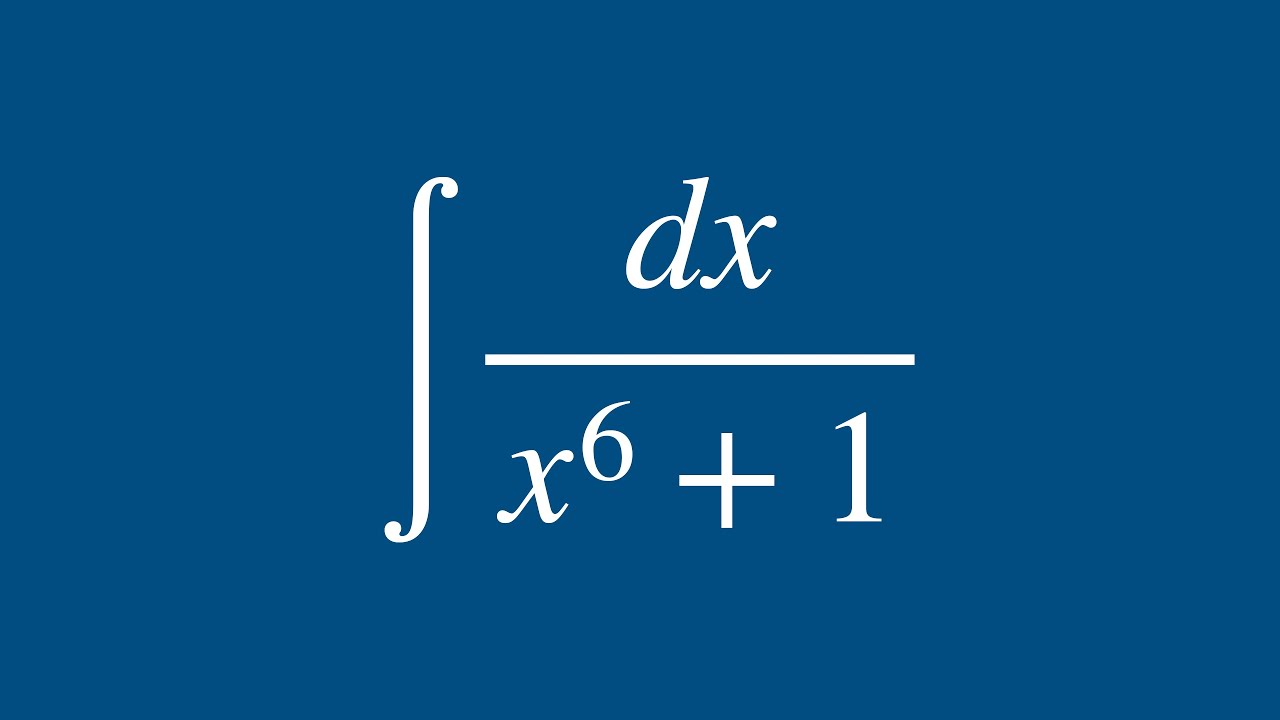
Показать описание
An absolutely filthy integral.
This Integral Will Surprise You
This integral will have you on the floor 🤣🤣
🔥INTEGRAL TRICK! Watch Till The End You Will Be Surprised! #calculus #integration #math
Integral with SURPRISE 😮ENDING! 🥳 #mathwithprofessorv #calculusvideos #integraloftheday #calculus...
This method is BEYOND helpful in integral problems! #calculus #mathhack #mathematics #mathchallenge
🔥Watch till the end you will be surprised! EASY INTEGRAL PROBLEM #calculus #integration #math
An unusual integral with two very different solutions?
I used a double integral to solve a single improper integral
Data Integration: The Hidden Weapon You're Ignoring
🔥Seems difficult, but actually a brilliant integral problem! (TRICKS) #calculus #integration #math...
Forgetting “+ C” When Integrating an Indefinite Integral #Shorts #math #calculus
This integral is RIDICULOUS
If You Own HBAR, XLM, or QNT - Big Changes Are COMING!
When I activate the Perfect Susano'o, everyone finally feels what the power of a god truly mean...
#YvesBergquist sheds light on AI's deep integration in Hollywood 🎬 #TheGrill2024
AN UNBELIEVABLE INTEGRAL!!!
The Bernoulli Integral is ridiculous
IITian Inside - Flash Integration and Surprise Integration 🔥❤️ #jee #iit #calculus #maths
Taming another terrifying integral
Feynman's Integral Trick with Math With Bad Drawings
🔥Don't do u substitution at the first step! Let's integral faster! #shorts #calculus #inte...
Integral of the Day: 9.1.23 |Trig Sub and By Parts! | Spicy Stuff! 🥵🌶️| Math with Professor V...
Evaluating Definite Integral w/ t-results
COUNTDOWN to 2025: FINAL INTEGRAL with a SURPRISE! 13 Integrals in 13 Days! | Math with Professor V
Комментарии
 0:01:33
0:01:33
 0:03:29
0:03:29
 0:00:51
0:00:51
 0:00:56
0:00:56
 0:01:00
0:01:00
 0:00:53
0:00:53
 0:08:01
0:08:01
 0:11:14
0:11:14
 0:28:45
0:28:45
 0:00:57
0:00:57
 0:00:07
0:00:07
 0:20:07
0:20:07
 0:25:01
0:25:01
 8:44:34
8:44:34
 0:00:57
0:00:57
 0:08:10
0:08:10
 0:10:00
0:10:00
 0:00:47
0:00:47
 0:08:13
0:08:13
 0:15:35
0:15:35
 0:00:57
0:00:57
 0:16:16
0:16:16
 0:11:59
0:11:59
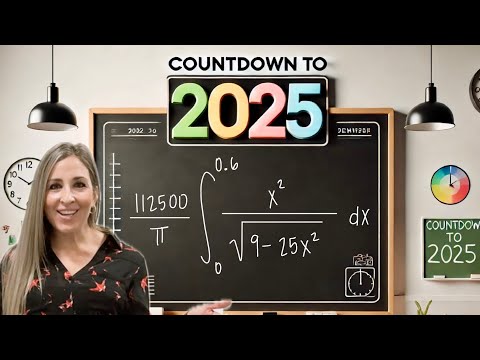 0:08:49
0:08:49