filmov
tv
Taming another terrifying integral

Показать описание
Here's an unexpected form for one of our favourite integrals. Incredible how symmetry can simplify such terrifying structures into familiar friends.
The gaussian integral evaluated using Feynman's trick:
The gaussian integral evaluated using Feynman's trick:
Taming another terrifying integral
MONSTER INTEGRAL EASILY TAMED
Look at what the Horse does when she cries... ❤
SHE PULLED THE SWORD OUT OF THE STONE RIGHT IN FRONT OF ME IN DISNEY WORLD
How Deathworlders Tamed the Galaxy’s Deadliest Beasts | HFY | Sci Fi Stories
stop any dog attack fast #smalldog
Transported to the Stone Age! I Bound a System – Complete Tasks for Generous Rewards! #manhwa
7 Orca Encounters That'll Brighten Your Day
Rebirth, The First Thing I Did Was Deceive My Friend into Giving Me an SSS Artifact Using a Coke!
Tame the Beast: Conquer the Challenge of Hard Integral
Giz tried to cheat and use Siri 😂 but came through in the end #talkingparrot #talkingbirds #shorts...
How to tell if a cat is playing or fighting.
I have the Billion-Fold Return System and have become the only immortal!
5 Signs You Have a Wounded Inner Child (How to Heal)
How To SURVIVE Dandy's World Christmas Twisteds...
Home Alone 1 & 2 Traps: Gruesome to Most Gruesome 🏡
7 Things You Must NEVER Do To Your Rottweiler Dog
After awakening my talent, ridiculed by everyone, because I awakened the peasant talent-part 2- FULL
After his rebirth, he summoned a giant centipede and rose up in the world of beast masters!
Solving ALL THE INTEGRALS from the 2022 MIT Integration Bee Finals
Make the wealthiest tycoons kneel, and hold the power of life and death over the highest elites!&apo...
How to manage your emotions
You Won't Believe What Happened After Humans Tame Wild Aliens! | HFY | Sci Fi Short Story |
I Shoplifted My Way to Another Million Dollars in Hydroneer
Комментарии
 0:08:13
0:08:13
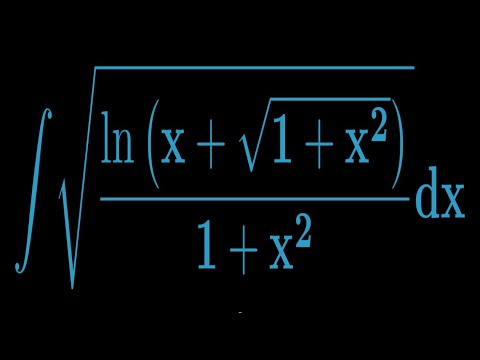 0:06:13
0:06:13
 0:00:25
0:00:25
 0:00:41
0:00:41
 0:32:30
0:32:30
 0:00:34
0:00:34
 10:38:58
10:38:58
 0:07:14
0:07:14
 21:24:55
21:24:55
 0:06:57
0:06:57
 0:00:25
0:00:25
 0:00:22
0:00:22
 8:48:08
8:48:08
 0:07:15
0:07:15
 0:08:02
0:08:02
 0:16:38
0:16:38
 0:06:02
0:06:02
 3:07:47
3:07:47
 12:00:00
12:00:00
 0:41:55
0:41:55
 9:46:53
9:46:53
 0:04:51
0:04:51
 0:09:28
0:09:28
 0:20:16
0:20:16