filmov
tv
AN UNBELIEVABLE INTEGRAL!!!
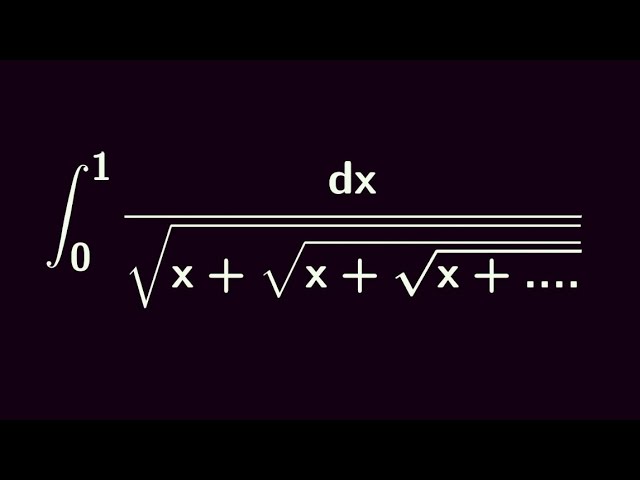
Показать описание
It's amazing how an infinitely nested integral like this is connected to a special constant like (sorry no spoilers 😂). Enjoy the video.
AN UNBELIEVABLE INTEGRAL!!!
An Unbelievable Integral | JEE Mathematics
UNBELIEVABLE calculus result using Feynman integration
7-Year-Old Math Whiz: Unbelievable Integration Problem Solved with Calculator! 🤯
Integral (part 1) Unbelievable Integral 8th century || integral formula proof #integral #maths #love
A gamma-digamma integral #calculus #gamma #advancedmaths #integral #integration #complexanalysis
Math is BROKEN: 1x2x3x...= √2π
Con man. Priest. Oil tycoon. Double Agent. An unbelievable, but true, story #shorts #podcastclip
NEW 2026 Corolla Cross First Look: Unbelievable Tech at an Unbelievable Price?
Unbelievable | Official Trailer | Netflix
Unlocking the Unbelievable Integration of the Human Mind
The UNBELIEVABLE Integration of AI into the Food Industry
Unbelievable Secret of Integration। Improper Integral । Mathematics by Dr. S.K. Sharma
The Unbelievable Integration Strategy of Turkey`s Air Power Revealed
Tesla's Unbelievable Integration of AI and Robotics #ai #shorts
Unbelievable Gadgets You Can’t Live Without!”
Unbelievable trick in integration #Cuet/#NDA/Class12 🔥🔥🔥🔥 #youtube ##youtubeshorts
The unbelievable camouflage
Unbelievable trick of definite integration problem.100%worked .Once watch.jee-main|advance
'Unbelievable and Rare Football Moment: The Most Jaw-Dropping Play You'll Ever See!'🔥...
A Unbelievable Incident: 'Emu War: Australia's Feathered Foe' #unbelievable #shorts #...
Integration tricks#shorts
Unbelievable Brain Implant Experience Seamless Technology Integration
Integration of trignometric functions using calculator
Комментарии
 0:08:10
0:08:10
 0:09:20
0:09:20
 0:14:58
0:14:58
 0:03:06
0:03:06
 0:01:56
0:01:56
 0:00:58
0:00:58
 0:00:59
0:00:59
 0:00:59
0:00:59
 0:02:17
0:02:17
 0:02:45
0:02:45
 0:00:51
0:00:51
 0:04:46
0:04:46
 0:04:43
0:04:43
 0:00:45
0:00:45
 0:00:39
0:00:39
 0:00:16
0:00:16
 0:00:55
0:00:55
 0:00:17
0:00:17
 0:09:36
0:09:36
 0:00:09
0:00:09
 0:00:49
0:00:49
 0:00:26
0:00:26
 0:00:45
0:00:45
 0:00:39
0:00:39