filmov
tv
Can You Solve x^x^x^... = 2? Infinite Exponent Tower Trick

Показать описание
What is the value of this infinite exponent tower?
See my follow-up video about a potential paradox 4 = 2:
I was asked this problem in a high school math competition, and you had to solve it as fast as possible. Hence I made a short 1 minute video showing this trick. For those wanting a proof suitable for a graduate level real analysis course (which is the only way to rigorously approach this problem), here are references.
Award winning paper Knoebel, R. Arthur. "Exponentials reiterated." The American Mathematical Monthly 88.4 (1981): 235-252.
Direct link to pdf:
Wikipedia tetration
False proof 2 equals 4
Math StackExchange links
If you like my videos, you can support me at Patreon:
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
If you buy from the links below I may receive a commission for sales. This has no effect on the price for you.
My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 3.8/5 stars on 31 reviews)
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 4.6/5 stars on 3 reviews)
"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.4/5 stars on 13 reviews.
"Math Puzzles Volume 2" is a sequel book with more great problems. (rated 4.3/5 stars on 4 reviews)
"Math Puzzles Volume 3" is the third in the series. (rated 3.8/5 stars on 5 reviews)
"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.3/5 stars on 12 reviews)
"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.7/5 stars on 4 reviews)
"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 5/5 stars on 3 reviews)
See my follow-up video about a potential paradox 4 = 2:
I was asked this problem in a high school math competition, and you had to solve it as fast as possible. Hence I made a short 1 minute video showing this trick. For those wanting a proof suitable for a graduate level real analysis course (which is the only way to rigorously approach this problem), here are references.
Award winning paper Knoebel, R. Arthur. "Exponentials reiterated." The American Mathematical Monthly 88.4 (1981): 235-252.
Direct link to pdf:
Wikipedia tetration
False proof 2 equals 4
Math StackExchange links
If you like my videos, you can support me at Patreon:
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
If you buy from the links below I may receive a commission for sales. This has no effect on the price for you.
My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 3.8/5 stars on 31 reviews)
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 4.6/5 stars on 3 reviews)
"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.4/5 stars on 13 reviews.
"Math Puzzles Volume 2" is a sequel book with more great problems. (rated 4.3/5 stars on 4 reviews)
"Math Puzzles Volume 3" is the third in the series. (rated 3.8/5 stars on 5 reviews)
"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.3/5 stars on 12 reviews)
"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.7/5 stars on 4 reviews)
"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 5/5 stars on 3 reviews)
Комментарии
 0:08:02
0:08:02
 0:12:08
0:12:08
 0:22:09
0:22:09
 0:04:53
0:04:53
 0:08:28
0:08:28
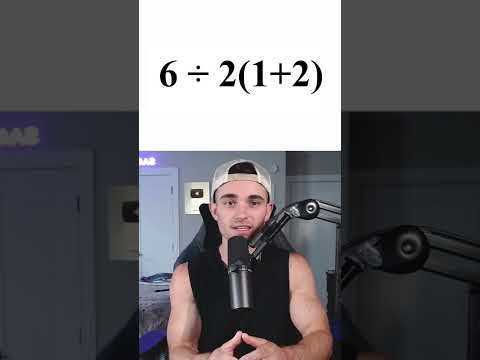 0:00:28
0:00:28
 0:11:08
0:11:08
 0:00:35
0:00:35
 0:12:02
0:12:02
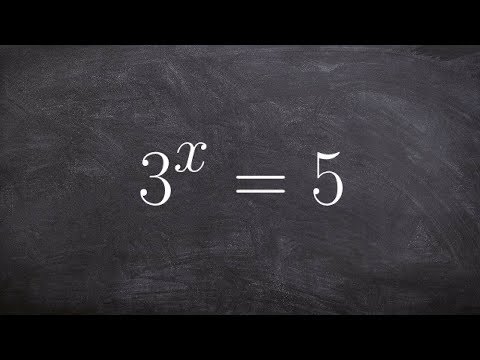 0:03:23
0:03:23
 0:09:43
0:09:43
 0:00:16
0:00:16
 0:00:36
0:00:36
 0:00:29
0:00:29
 0:00:29
0:00:29
 0:00:43
0:00:43
 0:08:01
0:08:01
 0:25:05
0:25:05
 0:08:11
0:08:11
 0:10:02
0:10:02
 0:00:20
0:00:20
 0:00:24
0:00:24
 0:09:04
0:09:04