Building Collision Simulations: An Introduction to Computer Graphics

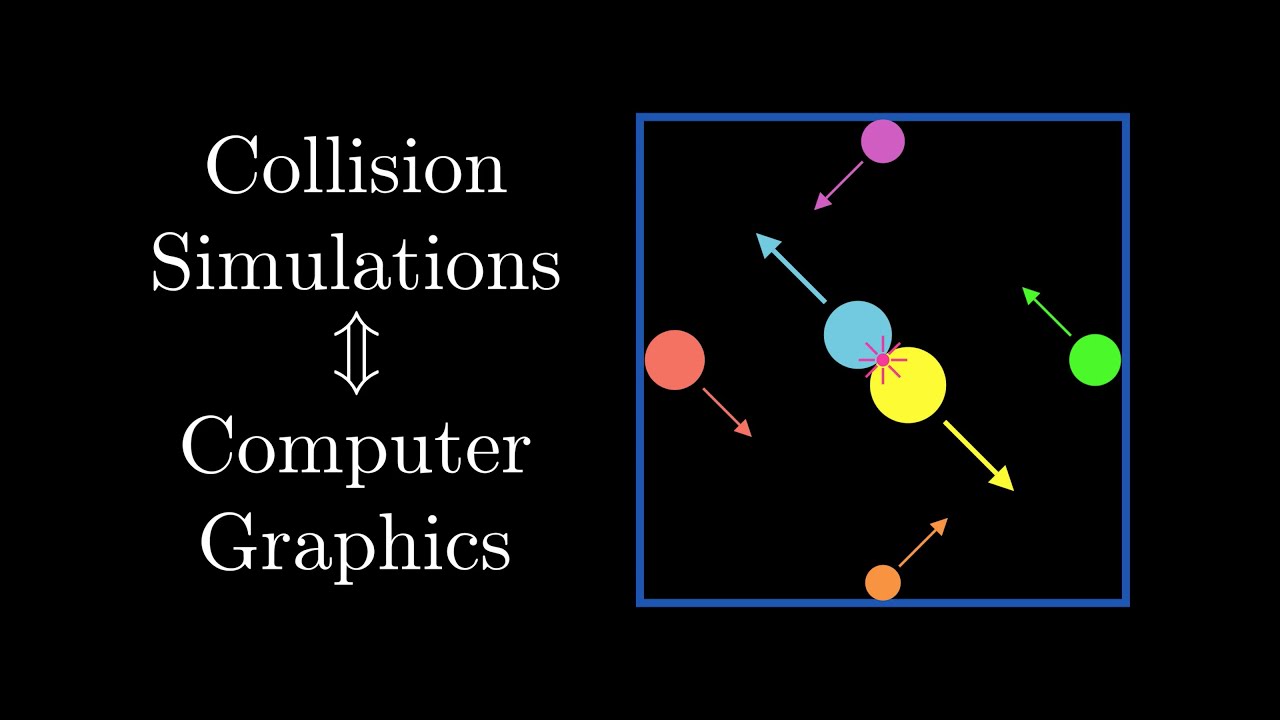
Collision detection systems show up in all sorts of video games and simulations. But how do you actually build these systems? Turns out that the key ideas behind these systems show up all over a field of computer science called computer graphics.

We start off with the basics of animation and then branch off into ideas in discrete and continuous collision detection. We break them down in the context of some simple simulations of a small number of particles, but scaling up these simulations is another challenge entirely. We present big ideas in broad phase optimization schemes for speeding up collision detection including the sweep and prune algorithm, uniform grids, K-D trees, and bounding volume hierarchies.

0:00 Introduction
1:25 Intro to Animation
2:46 Discrete Collision Detection and Response
5:50 Implementation
6:50 Discrete Collision Detection Limitations
8:10 Continuous Collision Detection
11:42 Two Particle Simulations
13:13 Scaling Up Simulations
15:42 Sweep and Prune Algorithm
19:05 Uniform Grid Space Partitioning
20:43 KD Trees
23:51 Bounding Volume Hierarchies
27:12 Recap

Correction: At 9:02, the linear interpolation equations should be x(t) = t * x(1) + (1 - t) * x(0) and y(t) = t * y(1) + (1 - t) * y(0). All subsequent derivations have the x(0) switched with x(1). All y(0) should also be switched with y(1) for the same reason.

Post-correction 2: I ran the experiment with the naive solution of checking every pair of particles with an added inefficiency in rendering the animations so the comparison wasn't fair and that's why the number was so high. The actual speed up is still fairly significant, but not THAT significant.

This video is supported by a community of Patreons
Special Thanks to the following Patreons:
Burt Humburg
Justin Hiester
Michael Nawenstein
Richard Wells
Zac Landis

The ideas and presentation in this video were inspired by a culmination of resources -- here are some that I found particularly nice for further exploration:
Game Physics Engine Development by Ian Millington Ch. 12

[Reducible]

Dumb mistake alert: At 9:02, the linear interpolation equations should be x(t) = t * x(1) + (1 - t) * x(0) and y(t) = t * y(1) + (1 - t) * y(0). All subsequent derivations have the x(0) switched with x(1). All y(0) should also be switched with y(1) for the same reason.

[NovaWarrior]

Thank you for:

A. Doing this work.
B. Making it free.

Awesome and inspiring.

[fncc]

This guy's voice feels like a mix of 3b1b and zach star

[Henrix]

28 minutes just flew by. Good job keeping viewers interested and focused

[eshh]

Just wow! Really speechless. I still can't believe that in just 30 minutes you were able to cover from the very basics of animation, i.e. the frame by frame rendering, to complex techniques like object and space partitioning.

Thank you soo much for these Amazinggg videos! Really looking forward to more CS Graphic and Animation oriented videos!

[MrDgf]

I was curious why the animation style was so similar to 3b1b, but I see from the description that he developed a custom library for animation for free use. Both of you guys are awesome.

[alegian]

Im studying computer science, and when I was still 15 years old I coded up my first app, a collision based game. I "re-invented" the first 10 minutes of the video on my own and got all the bugs you mentioned one by one but in the end it was so close to the paradigm I was taught in university :D

[SimulatingPhysics]

Hey, very nice explanation!
The Sweep and Prune algorithm offers a massive optimization despite how incredibly easy it is to implement. It's immensely useful in molecular dynamics along with the Bounding Volume boundary Hierarchy although the latter may be somewhat more tedious to implement.

[chinmay]

Thank you so much for covering this topic. You inspire me to study something new everyday. So wholesome. Thank you for doing everything. ❤️

[LorenzoValente]

Dude, your videos are pure gold. Computer Science students must LOVE you! Just a little note :D 2D particle-to-particle collision response closed formulas look hard and ugly, it is easier to deal with it by proceding by steps. First, split both v1 and v2 in two components, one parallel to the line of collision and the other tangent to it. You'll obtain 4 vectors: v1p, v1t, v2p and v2t. The final velocity vector for the first particle will be v1p + v2t, the final velocity vector for the second one will be v2p + v1t :) in other words: when two sphere collides, their velocity component tangent to the line of collision have to be swapped. This works if the two masses are the same but it is not that hard to take also that into account

[AwesTube]

I'm an animator professionally and it's fascinating to see the mathematical equivalent of all the processes I just intuitively do in my head. Great video!

[Andrewzero]

This video is a fountain of knowledge. I never knew how continuous collision worked, and how game engines optimized their physics. I've heard about k-d trees (and bi/quad/oct trees) but didn't know how k-d trees worked. Glad I found this!

[AwadMukbil]

1- One of the best teaching videos on YouTube in terms of quality and content
2- The best video that simplifies collision detection approaches

The guy is a genius! THANK YOU!!

[martindobrev]

For the grid aproach you can keep only cells with at least 1 object in them in set/map with hash function based on their coordinates. This will allow you to have very good resolution without big memory footprint .

[ptitbgdu]

I just discovered your channel since I am about to have a job interview for a PhD student position about collision detection in physics simulation in industrial mechanics softwares. I try to perfect my knowledge before I get there. Your work is simultaneously very beautiful to look, easy to follow and understand and also complete in the primary description of the problem. You have to continue in this direction it's objectively perfect. I immediately smashed the subscribe button :).

[CoughSyrup]

Fun fact: The tunneling problem is the reason that particles in this simulation that we are currently in, more commonly known as the universe, has a maximum speed limit--what we call the speed of light.

This also explains why we sometimes observe quantum tunneling effects to occur, if the barricade is made too thin. This is clearly a bug in the universe's source code, and as such I wouldn't recommend anyone building any technology that rely on that particular behavior of the universe, as it could become patched and change at any time, and without notice.

BTW, if anyone knows how to get in contact with the great creator, please let me know. I would be willing to submit a feature request on our behalf to improve the collision detection, with the intent of one day being able to lift this restriction on our physics. I presume the great creator employs some kind of bug tracking system and revision control... Or at least I desperately hope that is the case. Oh gawd--what if we were some kind of late night hack, hobbled together over the weekend and there was not even a backup made?!
Ah, existential dread... hello old friend.

[real]

Nice video! A programmer who sometimes writes simple games here, and still find this useful :)

Quick comment on the cons for uniform grid space partitioning approach: In fact having many empty grids isn’t a con if implemented with the right data structures.

One can maintain a list of grids, each associated to a list of intersecting objects, but skipping any empty grid:

1. Traverse each object, determine the list of (exactly or potentially) intersecting grids.
2. For each grid, push the object to a list associated to the grid. The latter can be achieved by creating a hash map which maps a grid (eg the key can be (row_id, column_id) for the 2D case).
3. Don’t bother initialize an empty list for each grid.
3. At the end, you can iterate through the hash map, skipping any grid with no intersecting objects.

One assumption here though is that at step 1, we need a relatively efficient algorithm to compute the list of all (or potential) intersecting grids. This is relatively simple to achieve for convex shapes like a circle (or a sphere in 3d space), but could get tricky for concave shapes where one might want to resort to approximating with a bounding box/volume.

[PedroCristian]

great presentation techniques. You started by Introducing the subject and giving a clear target at the end of video. You ended with a clear recap.

[AVUREDUES]

Oh my god, this is amazing! Even thought I’m on Patreon, I still watch the videos here for the sake of the algorithm (get it?), which is also why I comment filler words

[HadienReiRick]

13:23 you can see one of the blue particles in the right box getting stuck to a yellow particle and briefly getting slingshot around. same thing happens again at 14:37 between a red and yellow particle.


it looks like the reason this happens is that, during the 1st half of the simulation frame, when two particles are first moved, they penetrate each other at very grazing angles, the 2 particles overlap but already have velocities that would move them away from each other. the collision handling doesn't account for the fact that the two particles are already moving away from each other and just unconditionally reflect both particles' velocities along the collision normal. This results in the velocities deflecting slightly inwards to the opposing particle and remain nearly tangent to that particle's surface.

This continues until the particles reach a sweet spot frame when the next position update would fully depenetrate the 2 particles.