filmov
tv
Physics 62 Special Relativity (18 of 43) A Relativistic Time Experiment
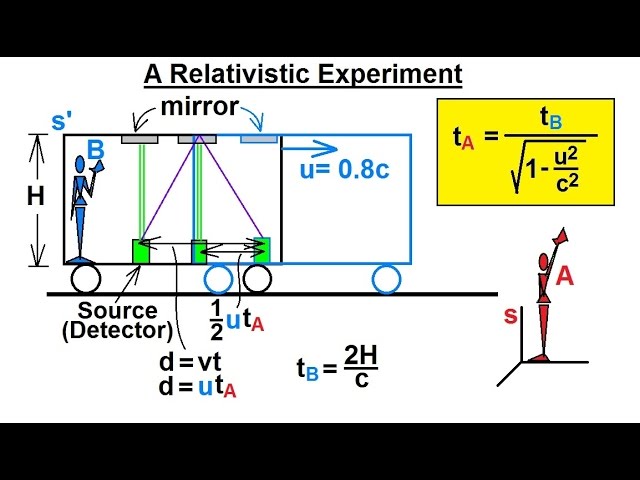
Показать описание
In this video I will explain and find t(relativistic)=? In a relativistic time experiment.
Next video in the Special Relativity series can be seen at:
Physics 62 Special Relativity (18 of 43) A Relativistic Time Experiment
Physics 62 Special Relativity (19 of 43) A Relativistic Length Experiment
Physics 62 Special Relativity (20 of 43) The Lorentz Transformation Equations: Length
Physics 62 Special Relativity (21 of 43) The Lorentz Transformation Equations: Time
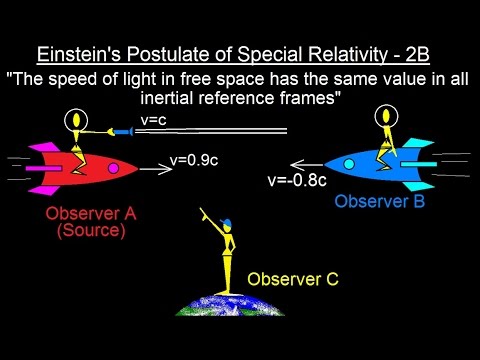
Physics 62 Special Relativity (15 of 43) Einstein's Postulate of Special Relativity - 2B
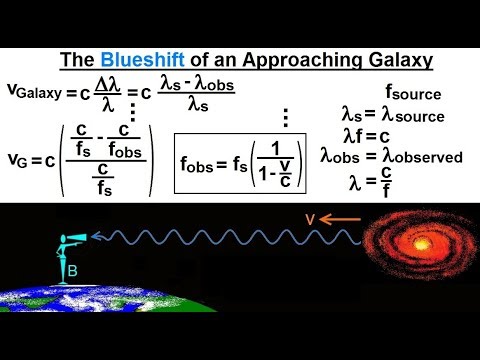
Physics 62.1 Understanding Space, Time & Relativity (18 of 55) Blueshift Approaching Galaxy
Physics 62 Special Relativity (13 of 43) Einstein's Postulate of Special Relativity - 1
Physics 62 Special Relativity (34 of 43) Relativistic Sample Problem - Length
Physics 62 Special Relativity (33 of 43) The Lorentz Factor Close-Up 2
Physics 62 Special Relativity (17 of 43) Galilean Transformation
Physics 62 Special Relativity (26 of 43) The Relativistic Doppler Effect for Light
Physics 62 Special Relativity (22 of 43) The Lorentz Transformation Equations:Length & Time Sum...
Physics 62 Special Relativity (39 of 43) Relativistic Sample Problem - Muon
Physics 62 Special Relativity (14 of 43) Einstein's Postulate of Special Relativity - 2A
Physics 62 Special Relativity (16 of 43) Einstein's Postulate of Special Relativity - 2C
Physics 62 Special Relativity (27 of 43) The Relativistic Units of Energy
Physics 62 Special Relativity (24 of 43) The Lorentz Transformation Equations: Velocity (v)
Physics 62 Special Relativity (25 of 43) The Lorentz Transformation Equations: Velocity (u)
Physics 62 Special Relativity (35 of 43) Relativistic Sample Problem - Time
Physics 62 Special Relativity (12 of 43) Momentum of a Photon
Physics 62 Special Relativity (28 of 43) The Relativistic Units of Mass
Physics 62 Special Relativity (31 of 43) The Relativistic Triangle Revisited
Physics 62 Special Relativity (38 of 43) Relativistic Sample Problem - Cosmic Radiation
Solving Problems on Time Dilation | Special Relativity | Physics problems
Комментарии
 0:11:29
0:11:29
 0:15:32
0:15:32
 0:03:23
0:03:23
 0:07:00
0:07:00
 0:04:12
0:04:12
 0:02:54
0:02:54
 0:05:42
0:05:42
 0:07:45
0:07:45
 0:04:47
0:04:47
 0:06:20
0:06:20
 0:09:16
0:09:16
 0:03:13
0:03:13
 0:03:22
0:03:22
 0:04:23
0:04:23
 0:03:34
0:03:34
 0:08:25
0:08:25
 0:03:12
0:03:12
 0:03:04
0:03:04
 0:07:52
0:07:52
 0:06:34
0:06:34
 0:03:36
0:03:36
 0:02:25
0:02:25
 0:11:28
0:11:28
 1:01:38
1:01:38