filmov
tv
Physics 62 Special Relativity (35 of 43) Relativistic Sample Problem - Time
Показать описание
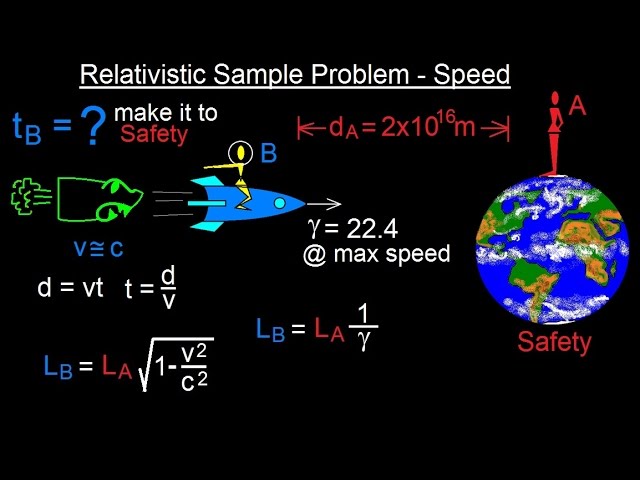
In this video I will finds time=? for a space ship, pursued by an enemy, to make it back to the safety of Earth.
Next video in the Special Relativity series can be seen at:
Physics 62 Special Relativity (35 of 43) Relativistic Sample Problem - Time
Physics 62 Special Relativity (34 of 43) Relativistic Sample Problem - Length
Physics 62 Special Relativity (36 of 43) Relativistic Sample Problem - Kinetic Energy
Physics 62 Special Relativity (30 of 43) The Relativistic Triangle
Physics 62 Special Relativity (32 of 43) The Lorentz Factor Close-Up
Physics 62 Special Relativity (27 of 43) The Relativistic Units of Energy
Physics 62 Special Relativity (37 of 43) Relativistic Sample Problem - Velocity
Chapter 35 — Special Relativity
Physics 62 Special Relativity (19 of 43) A Relativistic Length Experiment
Physics 62 Special Relativity (25 of 43) The Lorentz Transformation Equations: Velocity (u)
Physics 62 Special Relativity (24 of 43) The Lorentz Transformation Equations: Velocity (v)
Physics 62 Special Relativity (28 of 43) The Relativistic Units of Mass
Physics 62 Special Relativity (38 of 43) Relativistic Sample Problem - Cosmic Radiation
Physics 62 Special Relativity (33 of 43) The Lorentz Factor Close-Up 2
Physics 62 Special Relativity (16 of 43) Einstein's Postulate of Special Relativity - 2C
Physics 62 Special Relativity (29 of 43) The Relativistic Units of Momentum
Modern Physics, Lecture 17: Electricity & Magnetism in Special Relativity. General Relativity.
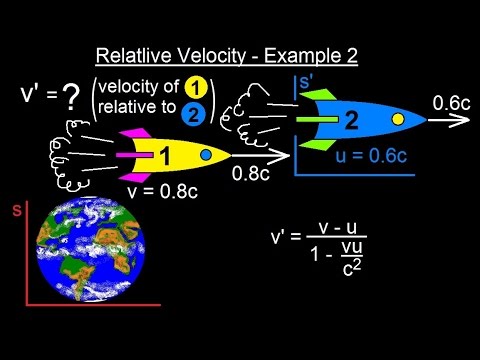
Physics 62 Special Relativity (42 of 43) Relative Velocity - Example 2
Physics 62 Special Relativity (41 of 43) Relative Velocity - Example 1
Physics 62 Special Relativity (43 of 43) Relative Velocity - Example 3
M-35. Force and energy in relativistic mechanics
Conservation of Relativistic Momentum and Energy: Special Relativity #8.1 | ZC OCW
Physics CH 0.5: Standard Units (34 of 41) Energy in Special Relativity
11 years later ❤️ @shrads
Комментарии
 0:07:52
0:07:52
 0:07:45
0:07:45
 0:06:51
0:06:51
 0:07:34
0:07:34
 0:07:19
0:07:19
 0:08:25
0:08:25
 0:05:10
0:05:10
 0:39:03
0:39:03
 0:15:32
0:15:32
 0:03:04
0:03:04
 0:03:12
0:03:12
 0:03:36
0:03:36
 0:11:28
0:11:28
 0:04:47
0:04:47
 0:03:34
0:03:34
 0:07:17
0:07:17
 0:52:44
0:52:44
 0:05:02
0:05:02
 0:06:00
0:06:00
 0:03:08
0:03:08
 0:24:32
0:24:32
 0:48:58
0:48:58
 0:07:00
0:07:00
 0:00:11
0:00:11