filmov
tv
Evaluating Limits by Rationalizing | Calculus 1

Показать описание
We find limits by rationalizing the numerator (or rationalizing the denominator, it works out very much the same). We'll do two examples, we'll find the limit of (sqrt(x-1)-1)/x as x approaches 0 and the limit of (sqrt(x+1)-2)/(x-3) as x approaches 3. #calculus1 #calculus
◉Textbooks I Like◉
★DONATE★
Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!
Follow Wrath of Math on...
◉Textbooks I Like◉
★DONATE★
Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!
Follow Wrath of Math on...
Evaluating Limits by Rationalizing | Calculus 1
Limits by rationalizing | Limits and continuity | AP Calculus AB | Khan Academy
Limits of Rational Functions - Fractions and Square Roots
[CALCULUS] Evaluating Limits using Conjugates (Rationalizing)
How to rationalize the radical to evaluate a limit
Limit Rationalize Both Numerator and Denominator to Find Limits
EVALUATING LIMITS BY RATIONALIZING
Calculus 1.3.2 Evaluating Limits By Dividing Out or Rationalizing
Evaluate Limit by Rationalization of Numerator
Solving Limits by Rationalizing! (Calculus 1)
Evaluating Limits With Fractions and Square Roots
Limits Using Rationalization
Evaluating limits by Conjugate Method - Limits and Radicals - Calculus
Evaluate Limit by Rationalizing Denominator
Evaluating a limit by rationalizing the radical
Evaluating Limits by Rationalizing | Calculus: Limits and Continuity
How to Compute a Limit by Rationalizing the Numerator
Evaluating Limits By Factoring
Evaluating Limits by Rationalizing the Numerator (Example)
How To Evaluate Limits of Radical Functions | Calculus
Finding Limits by Rationalizing the Numerator
Finding Limits by Rationalizing
L7: Evaluating Limit (Rationalizing Technique)
What is the Rationalizing Technique to Evaluating Limits - MCS21- Video 2
Комментарии
 0:06:38
0:06:38
 0:09:31
0:09:31
 0:10:06
0:10:06
![[CALCULUS] Evaluating Limits](https://i.ytimg.com/vi/0bK3iqkK6yE/hqdefault.jpg) 0:06:38
0:06:38
 0:02:47
0:02:47
 0:06:49
0:06:49
 0:08:03
0:08:03
 0:09:07
0:09:07
 0:07:13
0:07:13
 0:11:47
0:11:47
 0:11:42
0:11:42
 0:06:40
0:06:40
 0:16:51
0:16:51
 0:05:09
0:05:09
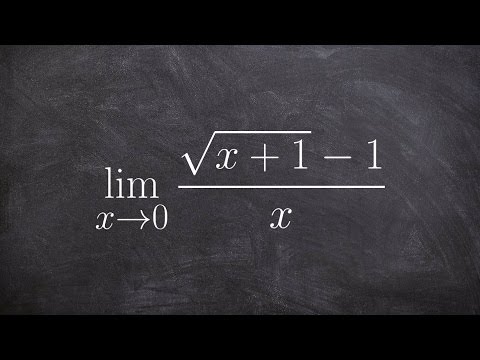 0:05:00
0:05:00
 0:13:10
0:13:10
 0:03:40
0:03:40
 0:11:35
0:11:35
 0:02:03
0:02:03
 0:10:39
0:10:39
 0:04:45
0:04:45
 0:06:22
0:06:22
 0:08:42
0:08:42
 0:03:34
0:03:34