filmov
tv
How To Evaluate Limits of Radical Functions | Calculus

Показать описание
This Calculus video tutorial explains how to evaluate limits with radical functions such as square root functions.
How To Evaluate Limits From a Graph:
Evaluating Limits By Factoring:
Limits of Rational Functions :
Limits of Radical Functions:
Limits of Trigonometric Functions:
___________________________________
How To Find The Limit at Infinity:
Infinite Limits + Vertical Asymptotes:
Limits at Infinity With Radicals:
Limits of Absolute Value Functions:
Limits of Composite Functions:
The Squeeze Theorem:
____________________________________
Limits and Logarithms:
Limits of Exponential Functions:
Piecewise Functions - Limits:
3 Step Continuity Test:
Continuity and Differentiability:
Limits - Test Review:
_____________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
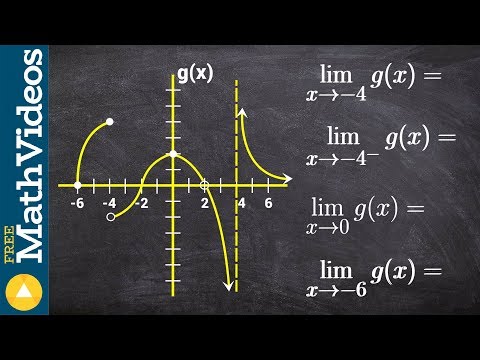
How To Evaluate Limits From a Graph:
Evaluating Limits By Factoring:
Limits of Rational Functions :
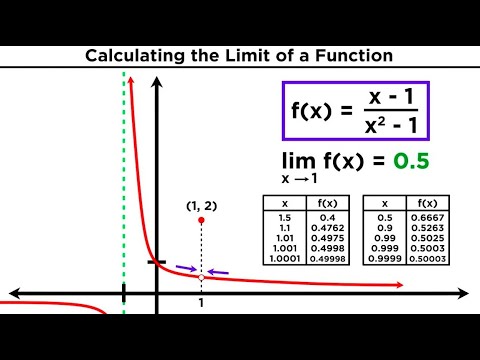
Limits of Radical Functions:
Limits of Trigonometric Functions:
___________________________________
How To Find The Limit at Infinity:
Infinite Limits + Vertical Asymptotes:
Limits at Infinity With Radicals:
Limits of Absolute Value Functions:
Limits of Composite Functions:
The Squeeze Theorem:
____________________________________
Limits and Logarithms:
Limits of Exponential Functions:
Piecewise Functions - Limits:
3 Step Continuity Test:
Continuity and Differentiability:
Limits - Test Review:
_____________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Комментарии
 0:11:35
0:11:35
 0:20:20
0:20:20
 0:11:32
0:11:32
 0:05:00
0:05:00
 0:07:41
0:07:41
 0:06:25
0:06:25
 0:10:39
0:10:39
 0:11:08
0:11:08
 0:15:11
0:15:11
 0:08:14
0:08:14
 0:05:34
0:05:34
 0:12:49
0:12:49
 0:05:13
0:05:13
 0:06:02
0:06:02
 0:11:42
0:11:42
 0:10:06
0:10:06
 0:10:06
0:10:06
 0:15:23
0:15:23
 0:17:44
0:17:44
 0:29:04
0:29:04
 0:10:35
0:10:35
 0:19:19
0:19:19
 0:15:09
0:15:09
 0:06:38
0:06:38