How to find the x values that make a horizontal tangent implicitly

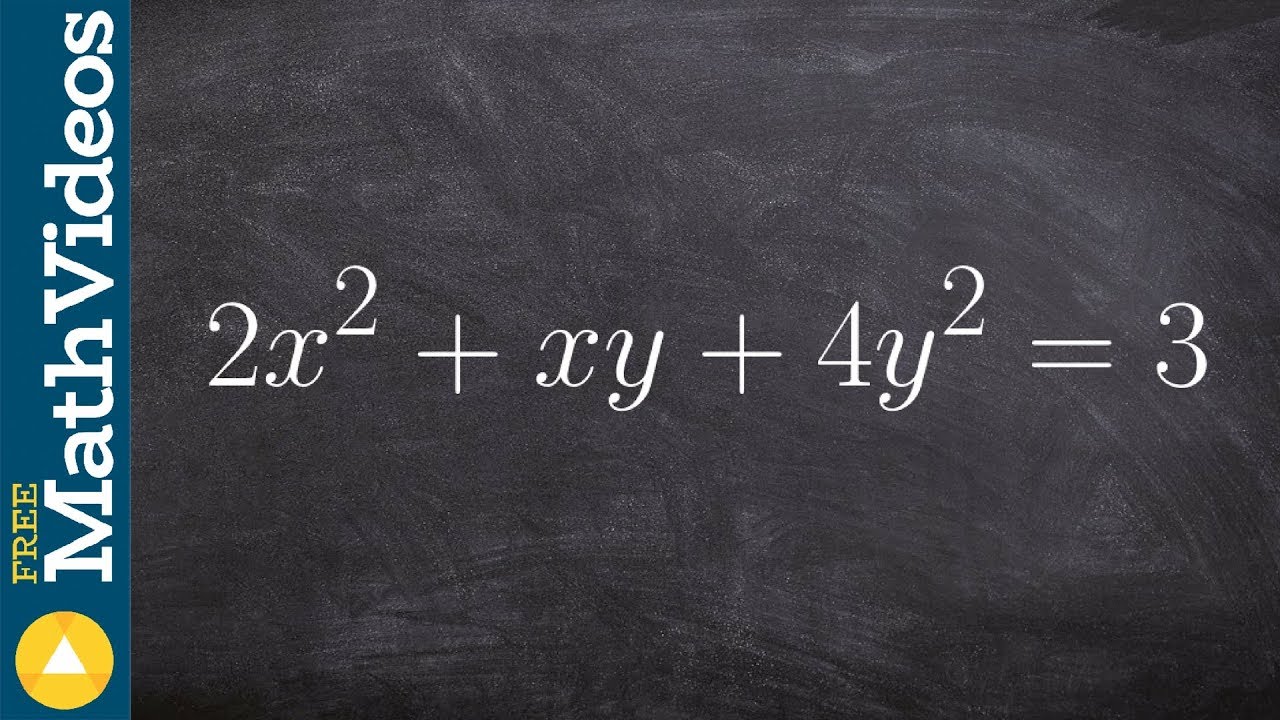
Показать описание

👉 Learn how to find the derivative of an implicit function. The derivative of a function, y = f(x), is the measure of the rate of change of the function, y, with respect to the variable x. The process of finding the derivative of a function is called differentiation.
A function is said to be implicit if the dependent variable is not explicitly defined in terms of the dependent variable. To differentiate a function in terms of another variable not used in the function, we differentiate both sides of the equality sign and then make use of the sum, product, and quotient rules of differentiation as the case may be to complete the differentiation.

Organized Videos:
✅The Derivative
✅Find the First and Second Derivatives of a Function
✅Find the Differentiability of a Function
✅Find the Derivative of Absolute Value Function
✅Find the Derivative of Exponential and Logarithmic Functions
✅Find the Derivative using Implicit Differentiation
✅Find the Derivative of Inverse Functions
✅Find the Point Where the Tagent Line is Horizontal
✅Write the Equation of the Tangent Line
✅Find the Derivative from a Table
✅Chain Rule Differentiation
✅Product Rule Derivatives
✅Find the Derivative of Trigonometric Functions
✅Find the Derivative using the Power Rule
✅Quotient Rule Derivatives
✅Solve Related Rates Problems

Connect with me:

#derivatives #brianmclogan