filmov
tv
Solving A Factorial Equation
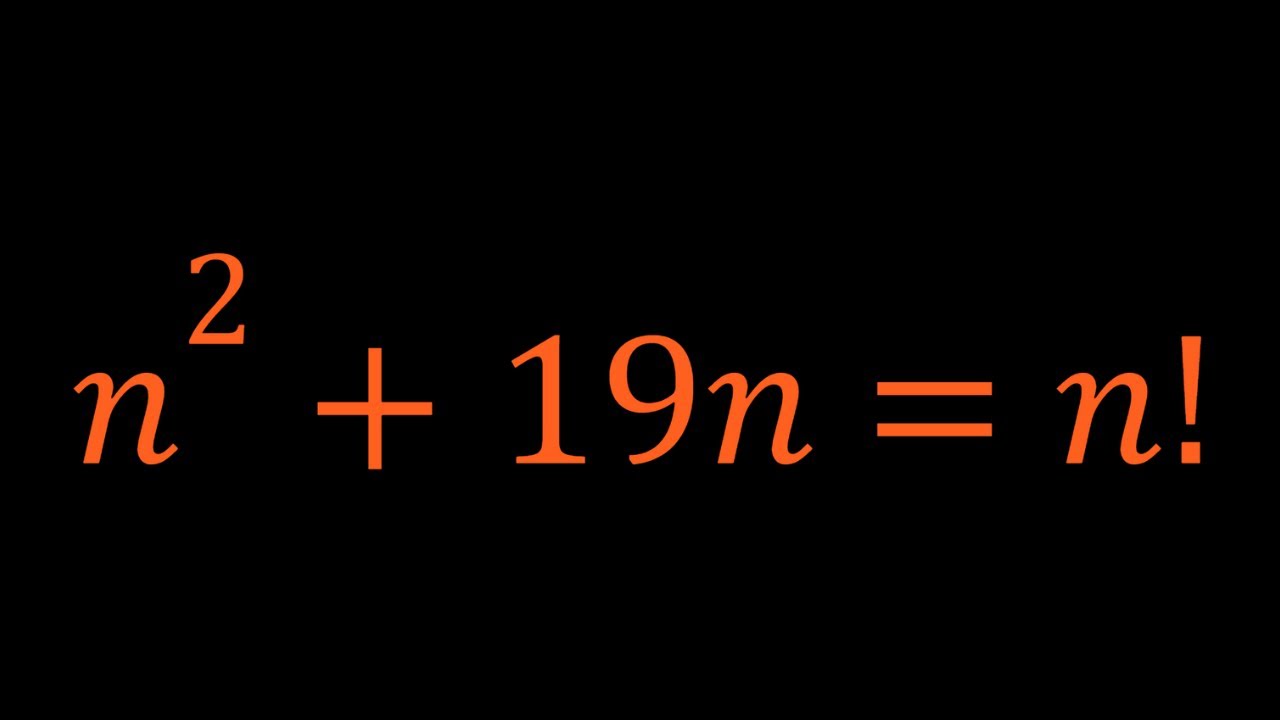
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#factorials #numbertheory #numbertheoryproblems
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#factorials #numbertheory #numbertheoryproblems
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solve Equation with Factorials
how to solve a factorial equation?
Can You Solve this Factorial Equation? | Fast & Easy Tutorial
Factorials Explained!
How to solve equations with Factorials
How to solve factorial equations
Solving Factorial Expressions in One Minute (2024) | Solve factorial equation
Solving A Nice Factorial Equation
Negative Remainder & Wilson Theorem | 90 Days UPSC CSAT 2025 Crash Course
A Nice Factorial Equation
Solve factorial equation
Nice Factorial Equation - Can You Solve It?
A nice factorial equation: The math behind solving equations.
Factorial Algebra Solve Equation Combinatorics
Can you solve it? | Factorial equation
Solving A Cool Factorial Equation: Math behind Solution
Solving Factorial Equation
Solving Factorial Equation
Can you solve it? | How to solve? | Factorial Equation
Solving A Factorial Equation #algebra #maths
Can You Solve This Factorial Equation | Solve for n | Number Theory
Solving A Factorial Equation | How To Solve Factorial Equation Without Using Mathematical Induction?
How to solve factorial equations?
Solving a Spectacular Factorial Equation | Algebra
Комментарии
 0:03:25
0:03:25
 0:02:22
0:02:22
 0:04:45
0:04:45
 0:11:17
0:11:17
 0:03:01
0:03:01
 0:03:34
0:03:34
 0:01:46
0:01:46
 0:03:19
0:03:19
 0:33:44
0:33:44
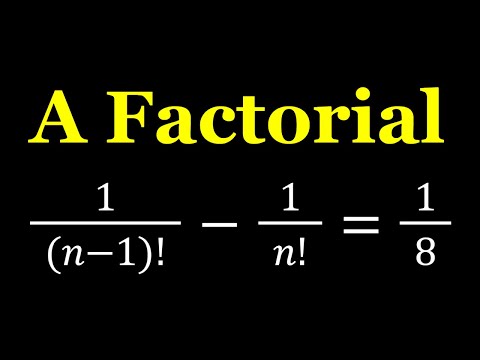 0:08:38
0:08:38
 0:06:31
0:06:31
 0:04:43
0:04:43
 0:10:54
0:10:54
 0:04:26
0:04:26
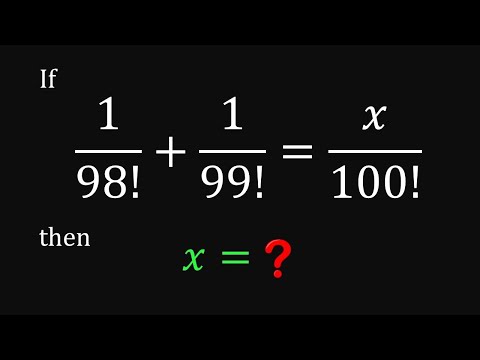 0:03:39
0:03:39
 0:10:52
0:10:52
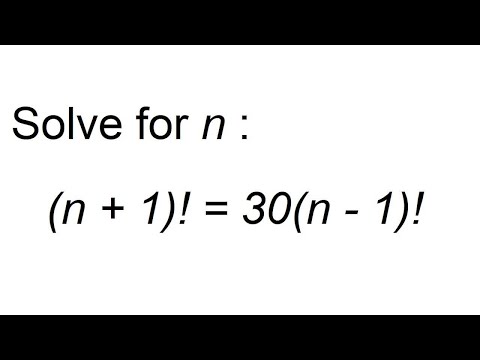 0:04:20
0:04:20
 0:02:44
0:02:44
 0:02:51
0:02:51
 0:00:39
0:00:39
 0:04:43
0:04:43
 0:05:09
0:05:09
 0:03:03
0:03:03
 0:08:37
0:08:37