Find the Limit of (x + x^3 + x^5)/(1 - x^2 + x^4) as x approaches Infinity

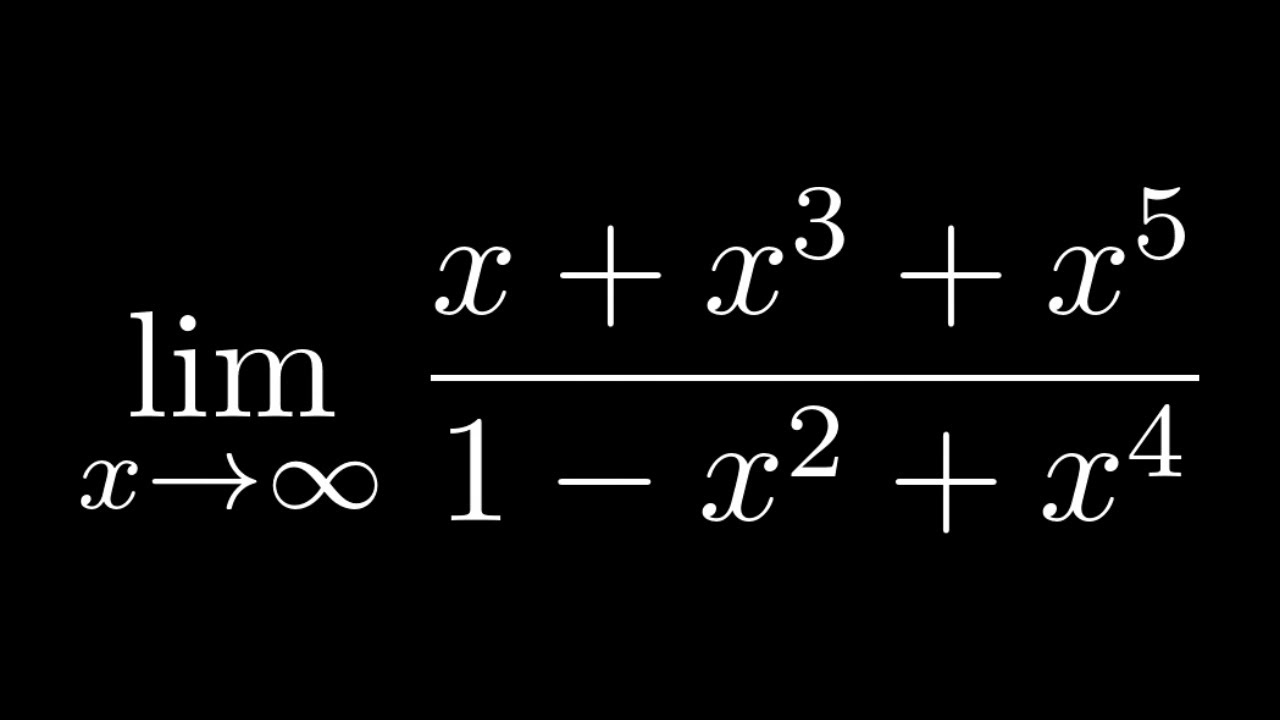
Показать описание

Find the Limit of (x + x^3 + x^5)/(1 - x^2 + x^4) as x approaches Infinity

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus 1 Lectures with Assignments and a Final Exam

Calculus Integration Insanity

Differential Equations Course

Differential Equations Lectures Course (Includes Assignments + Final Exam)

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Trigonometry 1 Course

Trigonometry 2 Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)

Рекомендации по теме

Комментарии

I was taught to divide the numerator and denominator by the highest order power in the denominator and then to just use limits normally.
Using l'hopital's rule 4 times would give lim x -> inf (5!x/4!) which is simple enough.
This method of largest exponentiation was refered to as a bit risky if you're not sure what type overpowers the others.

kozokosa

My Calculus teacher taught us this method but pointed out that this doesn't work in a few rare cases. He showed us the problem: limit x-> infinity sqrt(9x^2+x)-3x. If you attempt to ignore the +x term in the radical you will get limit x-> infinity sqrt(9x^2)-3x which should equal 0, but this is wrong and the actual answer is 1/6. If you instead multiply by the conjugate on the top and bottom and then proceed to ignore the +x term this time you will get the right answer of 1/6.

lavamob

We can also solve it by L' Hopital's rule

Maths_.

The actual answer is that it has no limit - you cannot approach infinity.

davidreynolds

We divide each term by the highest power of x and 1/x^r=0 so I thought it was 1.

joshuakennedy

Find the Limit of (x + x^3 + x^5)/(1 - x^2 + x^4) as x approaches Infinity

How To Find The Limit At Infinity

How to Find Any Limit (NancyPi)

Evaluating Limits By Factoring

Limit of x/(x^2 + 7x) as x approaches 0

How to Find the Limit at Infinity (NancyPi)

Find the Limit of (2 - x)/(x - 1)^2 as x approaches 1

Find the Limit of (x^4 + x^5) as x Approaches Negative Infinity

Learn how to evaluate a limit at infinity

LIMITS AND DERIVATIVES in 1 Shot | Maths | 1st PUC

Find the Limit of (x + x^3 + x^5)/(1 - x^2 + x^4) as x approaches Infinity

Find the Limit of (x - sqrt(x)) as x approaches infinity

Find the limit of (x - 1)/(x^2(x + 2)) as x approaches negative 2 from the right

Find the Limit of (1 - x)/(x^2 - 1) as x approaches 1

Limit as x goes to negative infinity AGAIN!

Limit of the xth root of x as x approaches infinity

Find the limit as x approaches pi/2. Right sided limit for e^(tan x) Natural exponential function

How to Find the Limit of the Cube Root of x as x Approaches Infinity #shorts

How to Find the Limit of the Square Root of x as x approaches Infinity #shorts

Find the Limit of sqrt(x) as x Approaches Infinity

How To Tell If The Limit Exists

limit as x approaches infinity of x/sqrt(x^2+1)

Find the Limit of (1/x - 1/|x|) as x approaches 0 from the left

This is a very famous limit

Calculus Limits at Infinity The Limit of x/sqrt(x^2 - x) as x approaches negative infinity