filmov
tv
How to Find the Limit at Infinity (NancyPi)
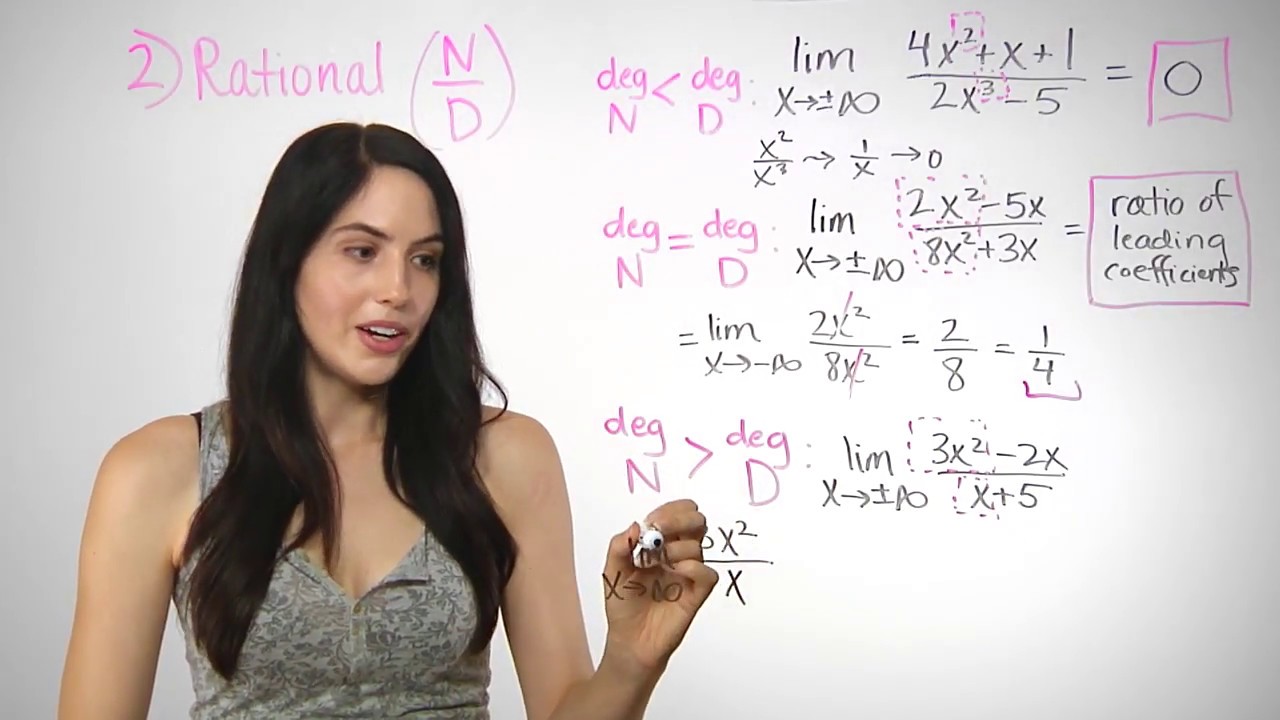
Показать описание
MIT grad shows how to find the limit as x approaches infinity or negative infinity. To skip ahead: 1) For a POLYNOMIAL or CONSTANT in the limit expression, skip to 1:56. 2) For a RATIONAL ("FRACTION") expression in the limit, skip to 8:49. 3) For something of the form (SINX)/X, skip to 23:01. and 4) For an EXPONENTIAL example, skip to 27:27. Nancy formerly of MathBFF explains the steps.
1) For a POLYNOMIAL or CONSTANT in the limit expression: the limit of a CONSTANT (just a finite number like 3), as x approaches infinity or negative infinity, will just be equal to that same constant number. For the limit of a POLYNOMIAL (such as 2x^2 + 2x + 5), as x approaches infinity or negative infinity, just focus on the leading term (highest x power term) in the polynomial, usually the first term. You can ignore all lower terms, because as x gets infinitely large (in either the positive or negative direction), the highest term is growing most quickly, and the lower terms will not affect the limit value. Then figure out whether this leading term will grow toward positive infinity or negative infinity, as x gets extremely large. For instance, if the leading term is 2x^2, as x goes to positive infinity, this leading term will also go toward positive infinity, and the limit will be positive infinity. If the leading term were -2x^2, the x^2 would go toward infinity, as x goes to infinity, but because of the -2, the limit is negative infinity. For X approaching NEGATIVE INFINITY, keep in mind that a negative number, to an even power, becomes positive. A negative number, to an odd power, stays negative. For instance, what if the leading term is 4x^3, and you want to find the limit as x goes to negative infinity? If you think of plugging in a very large negative number for x, the 4x^3 would still be large and negative because of the odd power. The term would go toward negative infinity, so you can write that the limit is equal to negative infinity.
2) For a RATIONAL ("FRACTION") expression in the limit: I show a shortcut (and also the official formal algebraic method) to find the limit, as x goes to infinity or negative infinity. For the SHORTCUT, there are three cases: 1) If the DEGREE OF THE NUMERATOR IS LESS THAN the degree of the denominator, then the limit is equal to zero, no matter if x is approaching positive infinity or negative infinity. 2) If the DEGREE OF THE NUMERATOR IS EQUAL TO the degree of the denominator, then the limit will be equal to the ratio of the coefficients of the leading terms of the numerator an denominator, no matter if x is approaching positive infinity or negative infinity. For instance, if you're finding the limit of the rational expression (2x^2 - 5x)/(8x^2 + 3x), as x tends toward infinity or negative infinity, the limit will be equal to the ratio 2/8, which simplifies to 1/4. The limit equals 1/4. 3) If the DEGREE OF THE NUMERATOR IS GREATER THAN the degree of the denominator, then the limit will be either infinity or negative infinity. For ex., to find the limit, as x approaches infinity, of (3x^2 - 2x)/(x + 5), instead focus on finding the limit of the ratio of leading terms, as x approaches infinity. So instead, you can find the limit of 3x^2/x, which simplifies to the limit of 3x, as x approaches infinity. Since 3x goes toward infinity, as x goes to infinity, the limit is infinity. NOTE: if x had instead been approaching negative infinity, the limit of the original expression would have been negative infinity, since 3x goes to neg. infinity as x tends to neg. infinity.
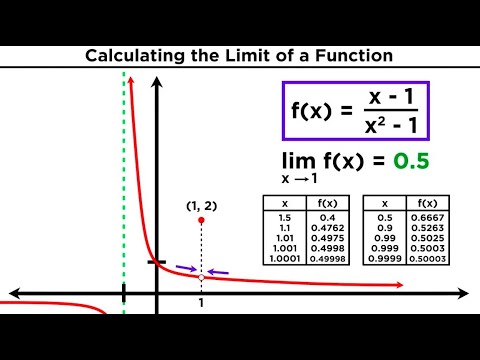
3) For something of the form (SIN X)/X: there is a trig property you can use to simplify: that the limit, as x approaches infinity or neg. infinity, of (sin x)/x is equal to 0. If your expression isn't exactly (sin x)/x but instead has something like 2x or 3x inside the sine function, like sin(3x) over x, you can use the same property but first have to rearrange the expression in a way that matches what you need. Be careful not to confuse this property with another, very similar, (sin x)/x expression for when x is approaching 0. That property states that the limit of (sin x)/x, as x approaches 0, is equal to 1. Check out my video on how to find the limit, at a finite value, for how to use that property.
4) For an EXPONENTIAL in your limit expression (with a negative power): for instance, if you are finding the limit, as x approaches infinity, of e^(-2x), first rewrite the expression using the reciprocal instead of the negative power, so 1/e^(2x). Then it is easier to see what happens as x gets extremely large and goes toward infinity. The e^(2x) gets extremely large, so 1 over a very large number will head toward zero, and the limit will be equal to 0.
1) For a POLYNOMIAL or CONSTANT in the limit expression: the limit of a CONSTANT (just a finite number like 3), as x approaches infinity or negative infinity, will just be equal to that same constant number. For the limit of a POLYNOMIAL (such as 2x^2 + 2x + 5), as x approaches infinity or negative infinity, just focus on the leading term (highest x power term) in the polynomial, usually the first term. You can ignore all lower terms, because as x gets infinitely large (in either the positive or negative direction), the highest term is growing most quickly, and the lower terms will not affect the limit value. Then figure out whether this leading term will grow toward positive infinity or negative infinity, as x gets extremely large. For instance, if the leading term is 2x^2, as x goes to positive infinity, this leading term will also go toward positive infinity, and the limit will be positive infinity. If the leading term were -2x^2, the x^2 would go toward infinity, as x goes to infinity, but because of the -2, the limit is negative infinity. For X approaching NEGATIVE INFINITY, keep in mind that a negative number, to an even power, becomes positive. A negative number, to an odd power, stays negative. For instance, what if the leading term is 4x^3, and you want to find the limit as x goes to negative infinity? If you think of plugging in a very large negative number for x, the 4x^3 would still be large and negative because of the odd power. The term would go toward negative infinity, so you can write that the limit is equal to negative infinity.
2) For a RATIONAL ("FRACTION") expression in the limit: I show a shortcut (and also the official formal algebraic method) to find the limit, as x goes to infinity or negative infinity. For the SHORTCUT, there are three cases: 1) If the DEGREE OF THE NUMERATOR IS LESS THAN the degree of the denominator, then the limit is equal to zero, no matter if x is approaching positive infinity or negative infinity. 2) If the DEGREE OF THE NUMERATOR IS EQUAL TO the degree of the denominator, then the limit will be equal to the ratio of the coefficients of the leading terms of the numerator an denominator, no matter if x is approaching positive infinity or negative infinity. For instance, if you're finding the limit of the rational expression (2x^2 - 5x)/(8x^2 + 3x), as x tends toward infinity or negative infinity, the limit will be equal to the ratio 2/8, which simplifies to 1/4. The limit equals 1/4. 3) If the DEGREE OF THE NUMERATOR IS GREATER THAN the degree of the denominator, then the limit will be either infinity or negative infinity. For ex., to find the limit, as x approaches infinity, of (3x^2 - 2x)/(x + 5), instead focus on finding the limit of the ratio of leading terms, as x approaches infinity. So instead, you can find the limit of 3x^2/x, which simplifies to the limit of 3x, as x approaches infinity. Since 3x goes toward infinity, as x goes to infinity, the limit is infinity. NOTE: if x had instead been approaching negative infinity, the limit of the original expression would have been negative infinity, since 3x goes to neg. infinity as x tends to neg. infinity.
3) For something of the form (SIN X)/X: there is a trig property you can use to simplify: that the limit, as x approaches infinity or neg. infinity, of (sin x)/x is equal to 0. If your expression isn't exactly (sin x)/x but instead has something like 2x or 3x inside the sine function, like sin(3x) over x, you can use the same property but first have to rearrange the expression in a way that matches what you need. Be careful not to confuse this property with another, very similar, (sin x)/x expression for when x is approaching 0. That property states that the limit of (sin x)/x, as x approaches 0, is equal to 1. Check out my video on how to find the limit, at a finite value, for how to use that property.
4) For an EXPONENTIAL in your limit expression (with a negative power): for instance, if you are finding the limit, as x approaches infinity, of e^(-2x), first rewrite the expression using the reciprocal instead of the negative power, so 1/e^(2x). Then it is easier to see what happens as x gets extremely large and goes toward infinity. The e^(2x) gets extremely large, so 1 over a very large number will head toward zero, and the limit will be equal to 0.
Комментарии
 0:20:20
0:20:20
 0:16:42
0:16:42
 0:13:14
0:13:14
 0:11:35
0:11:35
 0:07:41
0:07:41
 0:11:08
0:11:08
 0:11:32
0:11:32
 0:01:40
0:01:40
 0:01:37
0:01:37
 0:09:22
0:09:22
 0:08:14
0:08:14
 0:05:34
0:05:34
 0:22:28
0:22:28
 0:30:49
0:30:49
 0:29:04
0:29:04
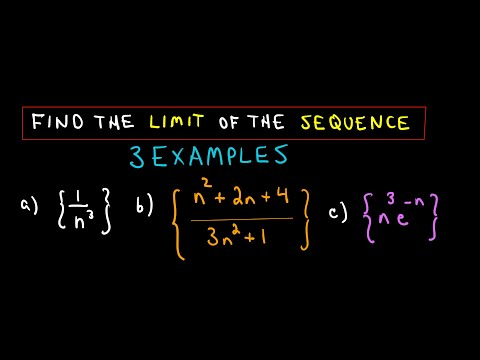 0:03:24
0:03:24
 0:01:49
0:01:49
 0:14:08
0:14:08
 0:19:19
0:19:19
 0:04:46
0:04:46
 0:12:49
0:12:49
 0:03:58
0:03:58
 0:02:00
0:02:00
 0:08:12
0:08:12