Solving an incredibly difficult problem!

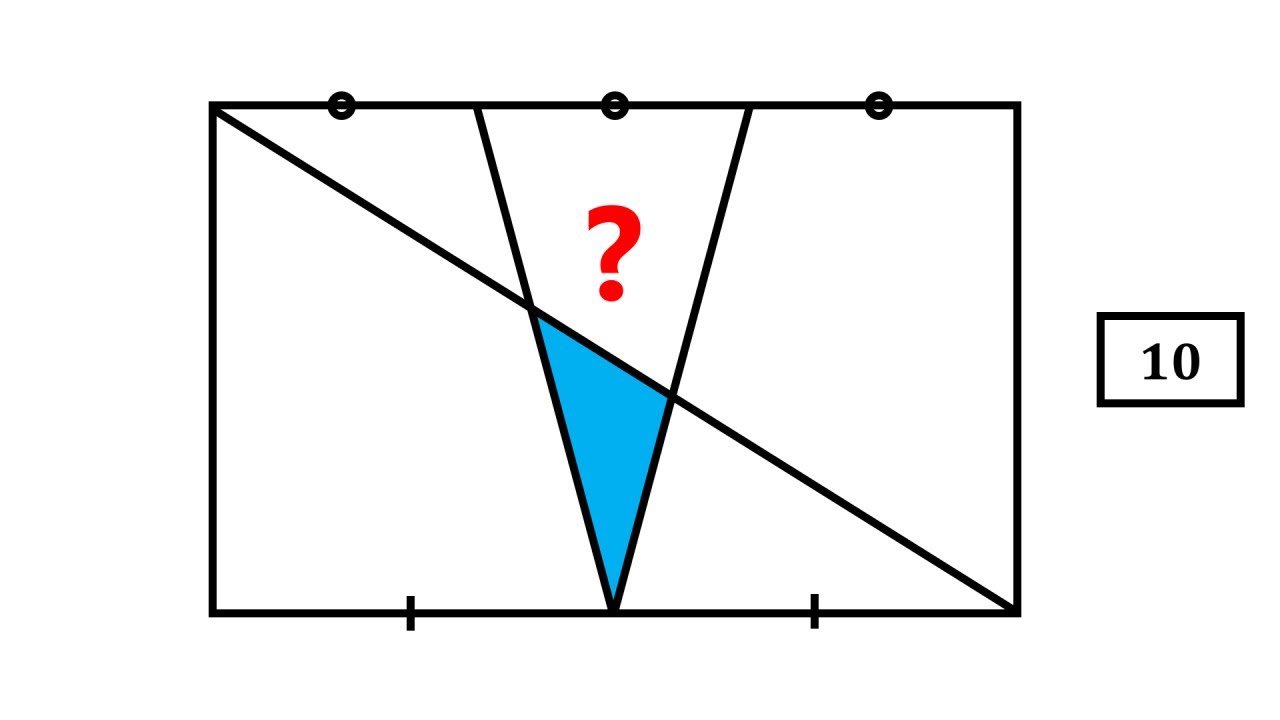
This problem seems like it is impossible to solve because it does not have enough information. If the rectangle has an area of 10, what is the area of the triangle?

After posting the video, I was told 2001 AMC 12 problem 22 was nearly the same problem:

Send me suggestions by email (address in video). I consider all ideas though can't always reply!

Like many YouTubers I use popular software to prepare my videos. You can search for animation software tutorials on YouTube to learn how to make videos. Be prepared--animation is time consuming and software can be expensive!

Why are there comments before the video is published? Get early access and support the channel on Patreon

If you buy from the links below I may receive a commission for sales. (As an Amazon Associate I earn from qualifying purchases.) This has no effect on the price for you.

Show your support! Get a mug, a t-shirt, and more at Teespring, the official site for Mind Your Decisions merchandise:

My Books (worldwide links)

My Books (US links)
Mind Your Decisions: Five Book Compilation
A collection of 5 books:
"The Joy of Game Theory" rated 4.1/5 stars on 97 reviews
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" rated 3.7/5 stars on 9 reviews
"40 Paradoxes in Logic, Probability, and Game Theory" rated 4.2/5 stars on 19 reviews
"The Best Mental Math Tricks" rated 4.3/5 stars on 21 reviews
"Multiply Numbers By Drawing Lines" rated 4.6/5 stars on 14 reviews

Mind Your Puzzles: Collection Of Volumes 1 To 3
A collection of 3 books:
"Math Puzzles Volume 1" rated 4.4/5 stars on 28 reviews
"Math Puzzles Volume 2" rated 4.4/5 stars on 9 reviews
"Math Puzzles Volume 3" rated 4.1/5 stars on 7 reviews

Connect with me

2017 Shorty Awards Nominee. Mind Your Decisions was nominated in the STEM category (Science, Technology, Engineering, and Math) along with eventual winner Bill Nye; finalists Adam Savage, Dr. Sandra Lee, Simone Giertz, Tim Peake, Unbox Therapy; and other nominees Elon Musk, Gizmoslip, Hope Jahren, Life Noggin, and Nerdwriter.

[MindYourDecisions]

I'm always amazed at the challenging problems assigned to young students! Here are some more videos you might enjoy (list below):

A gifted 10 year old student in China solved this in 1 minute:

Can You Solve Homework For 10 Year Olds In China?

Viral VERY HARD Problem For 11 Year Olds In China

Adults Stumped By Geometry Problems For 10 Year Olds. Can You Solve Them?

Can You Solve The Sand Mixing Riddle? (Homework For 10 Year Olds Singapore)

HARD Math Problem A 13 Year-Old Solved 1 Second! 2017 MathCounts Final Question

Can You Solve This Problem For 12 Year Olds In Singapore? 4 Overlapping Circles Puzzle

[edzejandehaan]

This problem was given to ten year olds? Ha, that's NOTHING, I gave this problem to a bunch of TWO year olds!
They didn't solve it either.

[thomashughes]

Yes, the problem was given to 10-year-olds, and they are now 20 and can solve it! ;)

[monkeseeaction]

There's an old trick to this kind of problems in case you don't want to do algebra. The fact that the problem doesn't give you any specific lengths or ratios of the rectangle's sides implies that the answer (assumed to exist) must be the same regardless of those conditions. Therefore you can just give the sides whatever lengths and proceed to compute the area without any unknowns. For example you can make it a square with each side's length equal to 1. You can use particular lengths that make the computation way easier. After you've obtained a number which is the area of the triangle under your assumption of the side lengths, and if your rectangle's area is not 10, simply scale the triangle area up by the ratio of your rectangle area to 10. This kind of tricks are common in Chinese middle and high schools that exploit lazy problem making. For example you can solve some very general and difficult problems quickly by making a triangle equilateral or certain angles right angles. The reasoning is that if the ultimate answer is assumed to be true regardless of certain conditions, then the answer obtained by bending those conditions to give you additional information that is not offered by the problem must also be true.

[fernandosantosviana]

maybe when i was 10 years old i was more inteligent, now i cannot solve it

[japeking]

I'm 72. I have just solved it after an overnight "cogitate sit" and now about an hour of slowly working out the areas of all the shapes inside the rectangle. I used the same similar triangles but instead of using ratio of their heights ( definitely the more clever way to go ) I used the ratio of their areas. Rather long-winded. I was surprised the area stayed constant no matter the perimeter but assumed that had to be the case given what information we had been supplied to solve the problem. Actually pleased with myself to ot there. Now I can go die in peace.

[commanderkuplar]

yeah and where in the world are 10 year olds learning this?!

[Surajmal]

Problem given to pregnant woman. Doctor asks the new born to solve the same problem.
Presh Talwalker: This problem was given to 10 min old baby.

[bobtivnan]

I’m a high school math teacher and it took me a half hour to figure it out. 10 year olds that can solve this are exceptionally bright. I used similar triangles like he showed and then used Cavalierie’s principle to find areas of the triangles. The key for me was to subdivide the whole rectangle into smaller rectangles whose areas can be found based on the side length ratios.

[SuperPassek]

Interesting solution.
Another solution is, at 2:19, we can use the area of the equilateral triangle is 1/6 of the area of the rectangle. As we computed the two edges of the target triangle are 3/5, 3/7 of the corresponding equilateral triangle edges, respectively, we get the area of the target triangle is 9/35, which is 3/70 of the rectangle, which is 3/7.

[rainerzufall]

Why is this wrong: We start with the area of 10 and then divide by:
3 to trisect the whole rectangle because we are focussing on the middle third of the rectangle
2 because we are only looking at half of that rectangle which is the triangle EFG
4 because the triangle we are looking for is a 4th of the big triangle.
So we end up with 10 devided by 24 which is close to this solution but not the same.
I somehow feel like the error is in the last step, but why? No matter how the line HI is drawn, it always goes through the center of the triangle and thus should devide the triangle in 1/4 and 3/4 even if it is not parallel to the bottom (or top in this case).

[MrHehe-qnzw]

I Solved it by Coordinate Geometry... It was long but easy...

[skeptic]

Interesting, the real answer of 3/7 is roughly 0.428. You can get very close to that by realizing that there are exactly 6 of the big triangles in the rectangle, and the area of the blue triangle is almost the same as the area if you rotate that diagonal (cc) on its center to be a horizontal line. Then you get a perfect fourth of that bigger triangle. So I estimated it to be approximately a quarter of a sixth, which is 5/12 which is 0.41666... and I can see visually that real answer is just a hair larger. So if this was a multiple choice answer, I'd be golden.

Did anyone else see this relationship?

[ReynaSingh]

i thought this video was finally gonna have problems that I could actually solve...

[legendofawesome]

I represented this on a co-ordinate plane. Recreated this diagram with the following equations:

X=5
Y=2
Y=2-2x/5
Y=12x/5-6
Y=6-12x/5

From there I prolly could have solved it using distance formula to get values I needed or something like that but I wanted to have some fun so I used integration by splitting the area in 2 pieces lol.

Anyways thought I'd share it its one of the few problems I've been able to solve on this channel 😅

[yunghuztler]

Just because something is given to solve doesn't mean it was solved

[JohnDlugosz]

I think 10-year-old kids are not given the problem cold like we are.
They have gone over several problems already with similar principles. They are taught how to solve them and the individual tools show up again and again. So the kid will see this and _know_ to start looking at all the triangles he can find (not just the ones mentioned in the puzzle) and sides that have known lengths.
They know to extend lines beyond the drawing because every pair of lines are parallel or intersect _somewhere_ . They know they can add more lines, anywhere they have defined points. They've seen examples before where the individual lengths are not known but a sum or product or difference is known, and can relate that combination to a geometric formula containing the same pattern.

[eylonshachmon]

You always say that this Chanel is one of the bests in YouTube, who told you so? It isn’t.

[smchoi]

A sketch of a co-geom. sol'n:

[1] Align the whole figure w/ the Cartesian plane s.t.
~ the corner of the rectangle (called R) where its side marked as bisected meets its marked diagonal is at (0, 0); &
~ the 2 sides meeting at the said corner lie on the +ve axes.
[2] Let s (resp. 6t) be the length of R's side on +ve x-axis (resp. +ve y-axis), so its endpoints are, ordered anticlockwise, at (0, 0), (s, 0), (s, 6t) & (0, 6t).
[3] As area of R = 10, 6st = 10 => st = 5/3.
[4] Coordinates of the vertex of the blue △ that is on the y-axis is G(0, 3t), while those of the "2 trisection points" on the side of R marked as trisected are F(s, 2t) & E(s, 4t).
[5] By slope-intercept form, eqn. of the line containing R's marked diagonal is L₁: y = (6t/s) x, whereas eqns. of the 2 lines, 1 of which containing GE & the other GF, are, respectively, L₂: y = (t/s) x + 3t & L₃: y = -(t/s) x + 3t.
[6] L₁ & L₂ intersect at (3s/5, 18t/5), while L₁ & L₃ intersect at (3s/7, 18t/7).
[7] By the "Shoelace Formula",
area of the blue △
| 0 3s/7 3s/5 0 |
= (1/2) | |
| 3t 18t/7 18t/5 3t |
= 9st/35 = 9(5/3)/35 = 3/7.

[Traonis]

So, in my opinion, there is a much easier way to solve this. (Using the letters added to the diagram for simplicity.)

1. Let x and y be the vertical and horizontal side lengths of the rectangle respectively. Construct the second diagonal of the rectangle from A to C and call the points where it intersects the triangle GFE I' and H'. (where the segment I I' is parallel to AD and H-H')

2. Note: The triangle GIH is equal to the two triangles I I' G and I' I H. Note: both of these triangles have a base I' I.

3. Therefore we can write the formula to find the area as: len(I' I) * height(I I' G)/2 + len(I' I) * height(I' I H)/2 which simplifies to len(I-I')/2 * (height (I' I H) + height ( I I' G)). Where height is measured in the y-direction (vertically).

4. to find (height (I' I H) + height ( I I' G)) which is just the length of the vertical line from AD to H, hereby called h. Look at the similar triangles GDH and BEH we get the following relationship h/(x/2) = (y - h) /(x/3).

4a. this simplifies to yx/2 - hx/2 = hx/3 --> y/2 = h/3 + h/2 --> y = 2h/3 + h --> y = (5/3)h --> h = (3/5)y.

5. to find len(I'I) consider the horizontal distance from AB to I', herby called w, and note that it is the same as the horizontal distance from CD to I. Therefore, the len(I-I') = x - 2w. To find w, we look at the similar triangles GDI and BIF to get the following relationship w/(x/2) = (x - w) / (2x/3).

5a. this simplifies to 2wx/3 = (x^2)/2 - wx/2 --> 2w/3 = x/2 - w/2 --> (2/3 + 1/2)w = x/2 --> (7/3)w = x --> w = (3/7)x

5b. Plugging that into our formula len(I-I') = x - 2w --> len(I' I) = x - 2((3/7))x --> len(I' I) = x/7

6. Finally, plugging that into our equation in (3.) we get (x/7)/2 * (3/5)y --> xy *(1/14 * 3/5) --> (because xy = 10) 10 * 1/14 * 3/5 = 1/7 * 3 = 3/7.