filmov
tv
Solving An Incredibly Hard Problem From Australia
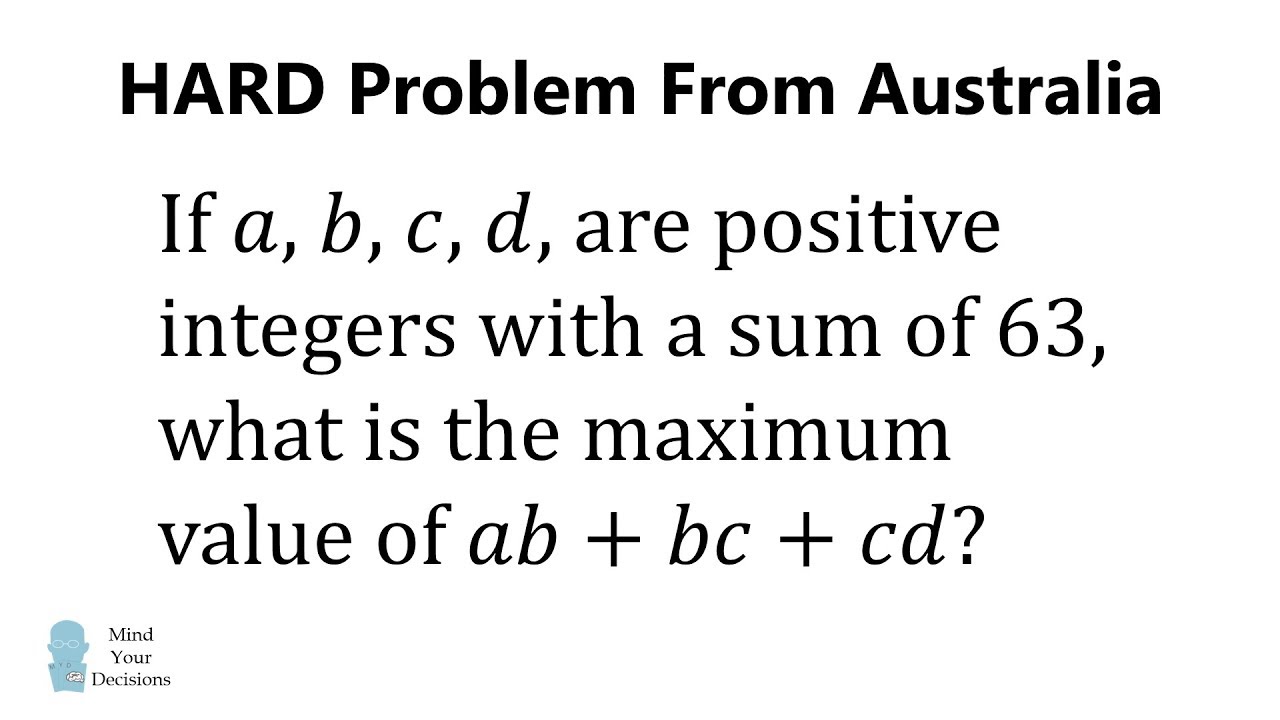
Показать описание
This problem stumped me! But it has a pretty nice solution. Thanks to all patrons! Special thanks this month to Kyle, Michael Anvari, Richard Ohnemus, Shrihari Puranik.
Source
Emailed to me about 2 years ago, traced to the Australian Intermediate Olympiad given in 2013.
Send me your favorite puzzles/suggestions by email (address in video). I get so many emails that I may not reply, but I save all suggestions.
This is the only channel to feature math topics suggested by people around the world. Support on Patreon to inspire mathematical discovery and make the world a better place:
If you buy from the links below I may receive a commission for sales. This has no effect on the price for you.
Show your support! Get a mug, a t-shirt, and more at Teespring, the official site for Mind Your Decisions merchandise:
My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 4.0/5 stars on 41 reviews)
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 3.5/5 stars on 4 reviews)
"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.4/5 stars on 13 reviews.
"Math Puzzles Volume 2" is a sequel book with more great problems. (rated 4.5/5 stars on 6 reviews)
"Math Puzzles Volume 3" is the third in the series. (rated 4/5 stars on 6 reviews)
"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.4/5 stars on 13 reviews)
"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.8/5 stars on 5 reviews)
"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 4.3/5 stars on 6 reviews)
Connect with me
Source
Emailed to me about 2 years ago, traced to the Australian Intermediate Olympiad given in 2013.
Send me your favorite puzzles/suggestions by email (address in video). I get so many emails that I may not reply, but I save all suggestions.
This is the only channel to feature math topics suggested by people around the world. Support on Patreon to inspire mathematical discovery and make the world a better place:
If you buy from the links below I may receive a commission for sales. This has no effect on the price for you.
Show your support! Get a mug, a t-shirt, and more at Teespring, the official site for Mind Your Decisions merchandise:
My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 4.0/5 stars on 41 reviews)
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 3.5/5 stars on 4 reviews)
"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.4/5 stars on 13 reviews.
"Math Puzzles Volume 2" is a sequel book with more great problems. (rated 4.5/5 stars on 6 reviews)
"Math Puzzles Volume 3" is the third in the series. (rated 4/5 stars on 6 reviews)
"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.4/5 stars on 13 reviews)
"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.8/5 stars on 5 reviews)
"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 4.3/5 stars on 6 reviews)
Connect with me
Комментарии
 0:05:25
0:05:25
 0:03:45
0:03:45
 0:22:09
0:22:09
 0:04:38
0:04:38
 0:07:27
0:07:27
 0:05:44
0:05:44
 0:11:15
0:11:15
 0:12:34
0:12:34
 0:03:50
0:03:50
 0:17:34
0:17:34
 0:11:26
0:11:26
 0:05:51
0:05:51
 0:05:51
0:05:51
 0:07:51
0:07:51
 0:03:21
0:03:21
 0:16:19
0:16:19
 0:05:10
0:05:10
 0:04:41
0:04:41
 0:09:24
0:09:24
 0:02:59
0:02:59
 0:04:16
0:04:16
 0:05:48
0:05:48
 0:04:32
0:04:32
 0:02:21
0:02:21