The Birthday Paradox

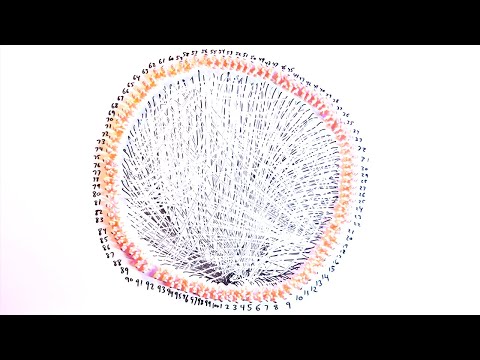
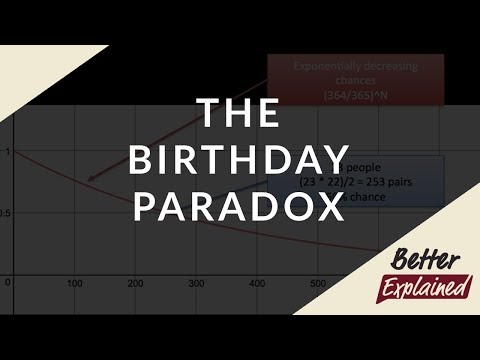
How many people need to be in a room before there’s a 50% chance that two of them share the same birthday? Is it about 180, since that’s around half of 365? Is it only 100? The real answer is surprisingly much, much smaller.

If you have just 23 people in a room, the odds of whether two get presents on the same day is a coin flip. Get 50 people together and that shared-birthday probability skyrockets to 97%. A handful more and it’s a virtual statistical certainty.

Really? Yes, really! With the aid of tiny plastic babies and some mathematics, Kevin proves and visualizes this surprising veridical paradox.

**** LINKS ****

Birthday Attack Example In Hacking

Birthday Attack Hash Collision

Hashing Algorithms And Security - Computerphile

Discussion On The Birthday Attack

The Birthday Attack

***********

Vsauce2 Links

Hosted, Produced, And Edited by Kevin Lieber

Research And Writing by Matthew Tabor

Huge Thanks To Paula Lieber

Get Vsauce's favorite science and math toys delivered to your door!

MY PODCAST -- THE CREATE UNKNOWN

[Vsauce]

Hey I just recently passed 4 million subscribers and just wanted to thank each and every one of you!!! Now if you'll excuse me I have a cup of babies to finish drinking.

[mkaylaC]

I feel like I just learned everything and forgot everything at the same time

[thejesuschrist]

You could say my birthday is a paradox.

[aqaisback]

I love when the intros are completely random due to the lack of context.
“I have 23 BABIES.”

[beepduck]

if you are in a room with 50 people, theres a pretty low chance that one of them will share your birthday, but a very high chance that at least two of the other people will have a shared birthday

[banquo]

To be fair, they're all babies so I assume their birthdays are fairly close together

[justin]

Man, imagine getting 100 people together to test this theory and then find out no one shares a birthday because you're so unlucky.

[maverick-rs]

Teacher: I have a math problem. Let's say you have 23 babies-
Me: A problem indeed.

[Beveyboygames]

There is a much better way for explaining this. Pretend you are in a room of 122 people excluding you, now you have a one in three chance of sharing a birthday with another person, because there are exactly as many people as one third the amount of days in a year, which is intuitive and makes sense. Now here's the trick EVERYONE has a one in three chance of sharing a birthday with someone else in this room because of the amount of people, now 99.99997% make more sense in a room of 100 people

[rhinoj]

"If we replace our birthday babies with online passwords, . . ." ( 5:18 )

I didn't expect to hear that sentence today

[satyakamshashwat]

Understood.. so basically, to make sure my password is secure, I should have at least 23 babies...

[bunbunnylopunny]

From a graduating class of around 23 people, the oldest and the youngest shared the same birthday just a year apart. No one else in the class did, just them. Pretty cool.

[Cam_uri]

My intrusive toughts are telling me to get 76 people that were born on diffrent days of the year and talk about this video being wrong

[Grandflea]

"I've got 23 babies"

Gengis Khan: *That's cute.*

[anthonythompson]

Wow. I did this as a fun experiment with some people in an online lobby. Turns out I had the same birthday as my twin brother

[WhiskeyPapa]

I remember doing this as an experiment in a math class with 26 people, and we had 2 sets of duplicate birthdays.

[besmart]

Kev, I have so much sympathy for you having to write on a dry erase board while left-handed. The struggle, it is real

[Alexdt]

ok so this is crazy, I asked like 9 people and turns out we all had birthdays this year, how do you even explain that?

[aviksheetdasgupta]

Kevin : "I've got 23 babies"
Me : Your wife, how is she ?

[ScKTM]

I had this problem in a statistic exam at computer science university, and yes... they asked us also if this paradox would have been useful for softwares and security was the answer. Very interesting topic