The Birthday Paradox

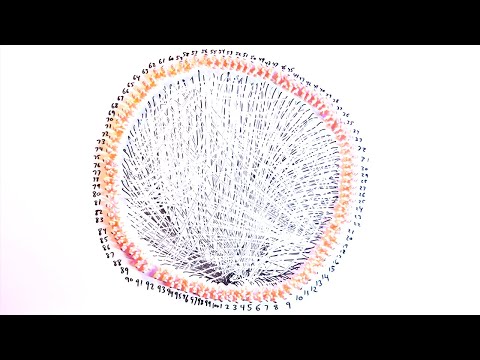
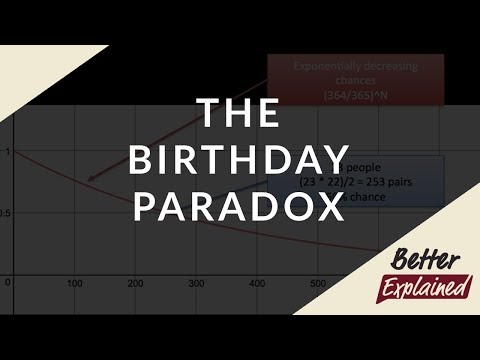
The Birthday Paradox says that only 23 people are needed for there to be a 50% chance a birthday is shared. Let's learn how!

~~~Sources and Music~~~

[celestevmoss]

Does anyone here share my birthday? 12/31

[PlayTheMind]

Here's the paradox flipped on its head: It's _incredibly_ unlikely that *365 people in a room* all have *different birthdays*

[Chew]

On the last boat I served on in the Navy one of my duties was UPC (Urinalysis Program Coordinator). As the UPC I had a database of all 140 crew members and the database included their birthdays. I had learned of the birthday paradox several years earlier so late one night on duty I played around with the database to find all the matching birthdays. There were 22 pairs of people who shared a birthday, 4 groups of 3 people who shared a birthday, and one group of 5 people who shared a birthday.

[Pfhorrest]

There are a lot of related misunderstandings that apply to everyday real life things. Like when the odds of something happening to SOMEONE, anyone at all, are one thing, and the odds of it happening to YOU SPECIFICALLY are another. For a toy example: the odds of someone at all winning a given raffle are 100%: some name or another is going to be drawn from the hat. But the odds of YOU IN PARTICULAR winning a raffle are much lower, decreasing as the number of participants increases.

Survivorship bias tends to factor into this in real life too. People say, "look at all of these people succeeding against apparently-improbably odds all the time! I'll just do that and I'll probably succeed too!", neglecting to compare how many people DIDN'T succeed when trying that, and so what the (low) odds of any PARTICULAR random person (like you) succeeding are, vs the (much higher) odds that just SOMEONE or another (but probably not you) will succeed.

[vm]

This is really cool!! We actually did this same problem on a homework for my AP Calculus AB class, but we only talked about it computationally, not conceptually. This video did an awesome job filling that understanding gap for me. Awesome content! (as always)

[Chew]

The Monty Hall Problem is going to blow your mind.

[louisng]

If there are zero people in the room, then any two random people selected from the room will definitely have the same birthday.

[himynameisnickolas]

I knew of the mathematics of this thing before but seeing the diagram made it make more sense why it’s true

[lpkzc]

I'm trying to figure out how to implement this idea into a party ice breaker.

In a room of about 40-50 people I could give a condensed version of this paradox. The first person to find an original pair of bdays wins a prize.

Ideas?

[izzy]

In my (admittedly short) 16 years, I've met/know of precisely 4 people who share my birthday

[Chribeify]

To get the right answer you would have to take 1 - "e" to the power of - possible combinations divided by a year.

[ScottWorthington]

Hi Matt. I had heard this before and kinda followed the math, but you did a really good job of presenting the info in a way that I can actually understand it. I think.

Now, what do ya know about quantum mechanics? 😃

[AmoebaMan]

Calling it a paradox seems weird. Aren't paradoxes usually things that cannot be explained?

[pichurro]

Hello. The paradox of birthday is very well known but  refers to at least two people.
Then, what is the probability if at least 3 people or "N" people different from 2 have the same birthday? Thank you.

[youssefmohamed-jtqp]

bro you are amazing thank you soooo much

[ElchiKing]

To me, this was never really a paradox, since I'm biased in a way that in my elementary school class of about 20 people, there were at least two people with the same birthday (I think it have been even more shared birthdays). Coincidentally, my cousin and two persons I met later also shared that exact birthday [and I don't really know many birthdates...]. Even more interesting: All of these people except my cousin were even born in the same year.

And somehow my family managed to have birthdays close together: My mother's birthday is 3 days before my brother's, my aunt's birthday is the day after her son's which is coincidentally the same as my uncle's (not her husband) birthday...

[samrodriguez]

Love your content still man! Keep it up. Also love that nerdfighteria flag! DFTBA!

[rondommicksay]

So my birthday is 10/21 and I’ve met 1 person that shares my birthday

[Ruby_V_]

I'll try to explain how I understand it, but mind you that I am still a probability noob as well.

Your second calculation doesn't work out because you failed to account for each additional person in the room shrinking the probability space. IE, following your second method, there would still be a non-zero probability that there isn't a shared birthday at 367 people.

[kalmar]

I understood it to the point of "we add the odds together". Cool. Then we substract them from one. Why tho? I'm terrible at math so that part... kinda seems arbitrary