filmov
tv
Find the Area of the Triangle | Quick Trick | 3 Easy Methods

Показать описание
Math Antics - Area
Finding the Area of a Composite Figure | Area of Composite Rectangles
Area for Kids
How to Find the Area of a Rectangle | Math with Mr. J
Find the Area Challenge
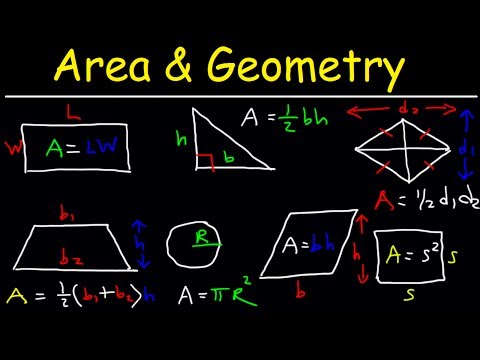
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
How to Find the Area of a Square | Math with Mr. J
Area of a Circle | MathHelp.com
Area of Parallelograms | How to Find the Area of a Parallelogram
Area and Perimeter
Area of a Trapezoid (Trapezium) | Math with Mr. J
How to Find the Area of Rectangles and Squares | Math with Mr. J
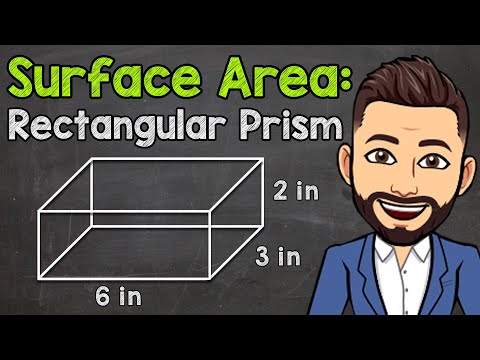
How to Find the Surface Area of a Rectangular Prism | Math with Mr. J
How to Find the Area of a Circle | Area of a Circle Step by Step
How to Find the Area and Perimeter of a Triangle | Math with Mr. J
(MATH) How to Find an Area of a Square? | #iQuestionPH
How to Find the Area of the Shaded Region | Square in a Square | Math with Mr. J
How to Find the Area of a Composite Shape | L-Shaped Example | Math with Mr. J
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Ex: Find the Area of an L-Shaped Polygon Involving Whole Numbers
How to Find the Area of the Shaded Region | Triangle in a Square | Math with Mr. J
How to Find the Area of a Circle Given the Radius | Math with Mr. J
Math Antics - Circles, Circumference And Area
Комментарии
 0:10:26
0:10:26
 0:07:14
0:07:14
 0:08:58
0:08:58
 0:04:43
0:04:43
 0:04:33
0:04:33
 0:20:35
0:20:35
 0:22:10
0:22:10
 0:02:48
0:02:48
 0:01:40
0:01:40
 0:04:30
0:04:30
 0:17:49
0:17:49
 0:06:14
0:06:14
 0:06:57
0:06:57
 0:04:57
0:04:57
 0:06:39
0:06:39
 0:05:48
0:05:48
 0:03:05
0:03:05
 0:03:32
0:03:32
 0:05:21
0:05:21
 0:06:37
0:06:37
 0:03:20
0:03:20
 0:04:18
0:04:18
 0:05:42
0:05:42
 0:07:56
0:07:56