filmov
tv
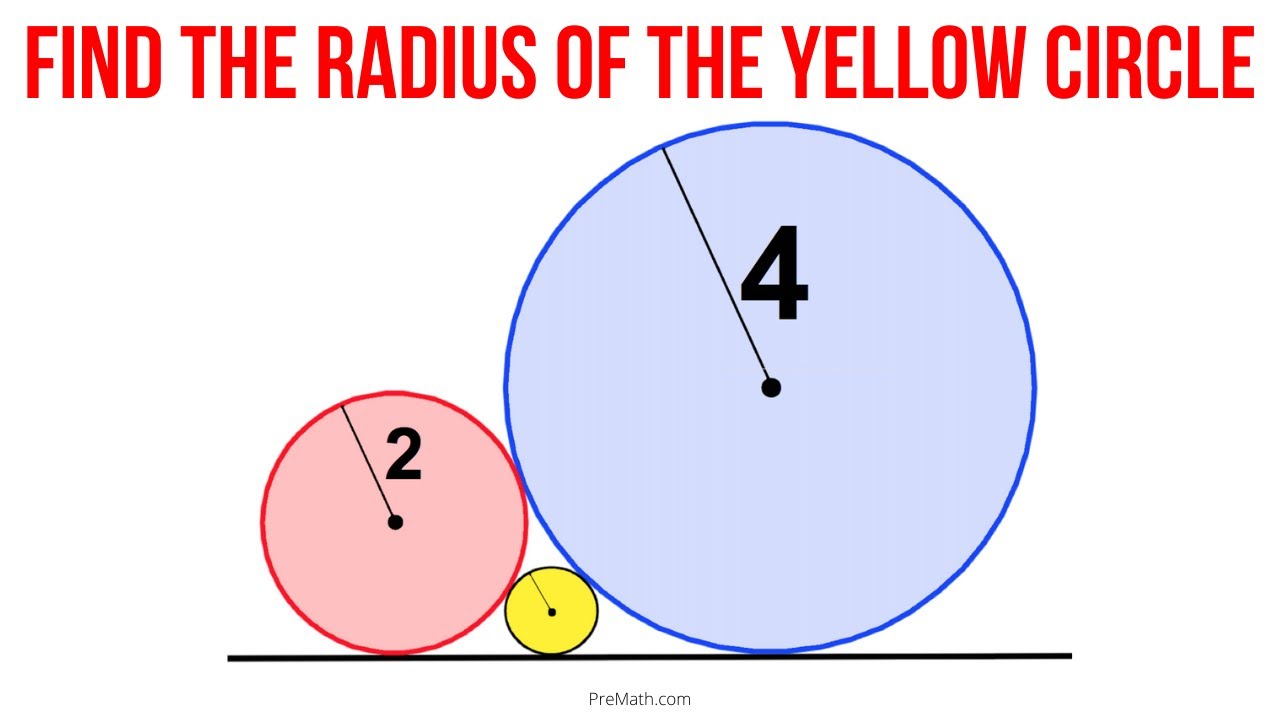
Can You Find the Radius of the Small Yellow Circle? | Step-by-Step Explanation
Показать описание
Can you find the Radius of the circle? | (Triangle inscribed in a circle) | #math #maths
Finding the Radius of a Circle Given the Diameter | Math with Mr. J
How to Find Radius of Circle from Area | Geometry
Find the Radius
Can You Find the Radius of the Small Yellow Circle? | Step-by-Step Explanation
Finding the radius when given the circumference
How to Find the Radius of a Circle (Circumference Given)
Can you find the Radius of the circle? | (Chord) | #math #maths | #geometry
Compass Tips - Find the center of a circle with an unknown radius
Can You Find the Radius of the Small Purple Circle? | Quick & Easy Explanation
Can you apply three methods to find the Radius of the circle? | Important Geometry skills explained
What is the Radius of a Circle? | What is the Diameter of a Circle? | Radius and Diameter Explained
Can You Find the Radius of the Circle? | Quick & Simple Tutorial
Finding the Radius of a Circle from an Equation
Can You Find the Radius of the Blue Circle? Two Methods Explained
Can you calculate the Radius of the Circle? | (Square) | #math #maths | #geometry
How to Find The Radius Of Circle
Given the area of a circle find the radius
Can You Find The Radius Of This Circle?
HOW TO FIND A RADIUS IN A CIRCLE / ARC
How to calculate the RADIUS, DIAMETER and the CIRCUMFERENCE of a circle
Learn 3 Different Methods to Find the Radius of a Circle | In-Depth Explanation
Can you find the Radius of the circumscribed circle? | (In-depth Proof) | #math #maths | #geometry
find the radius of circle whose diameter is 12cm #shorts #radiusofcircle
Комментарии
 0:10:25
0:10:25
 0:02:56
0:02:56
 0:05:03
0:05:03
 0:03:25
0:03:25
 0:15:47
0:15:47
 0:01:51
0:01:51
 0:01:02
0:01:02
 0:09:50
0:09:50
 0:01:13
0:01:13
 0:06:32
0:06:32
 0:11:12
0:11:12
 0:03:52
0:03:52
 0:09:15
0:09:15
 0:00:56
0:00:56
 0:13:04
0:13:04
 0:12:55
0:12:55
 0:02:05
0:02:05
 0:02:20
0:02:20
 0:02:41
0:02:41
 0:02:08
0:02:08
 0:08:14
0:08:14
 0:17:28
0:17:28
 0:09:52
0:09:52
 0:00:36
0:00:36