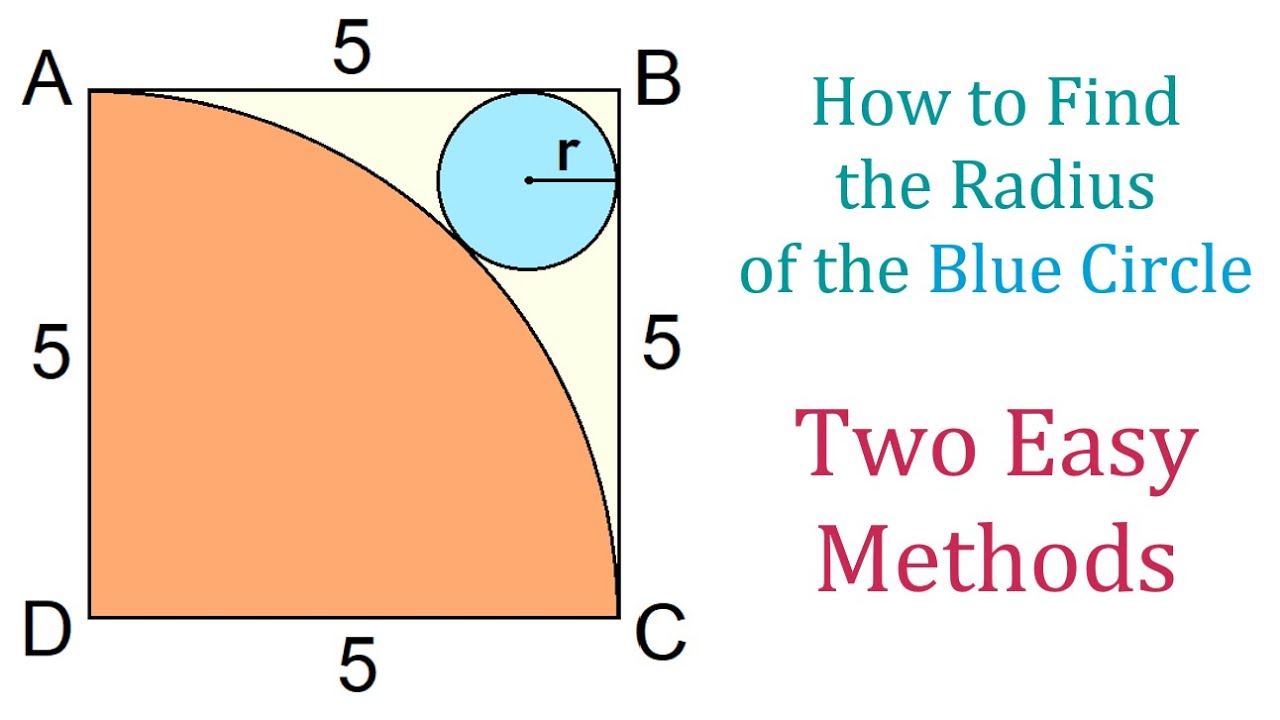
Can You Find the Radius of the Blue Circle? Two Methods Explained

The two methods involve the Pythagorean Theorem, Quadratic Formula, and rationalizing the denominator using the conjugate.

[اممدنحمظ]

تمرين جميل جيد . رسم واضح مرتب . شرح واضح مرتب . شكرا جزيلا لكم والله يحفظكم ويرعاكم ويحميكم جميعا. تحياتنا لكم من غزة فلسطين

[thesoundofsilence]

Lovely. I was more familiar with the 2nd method. She took a long route though solving for r.Establish your formula 5+r+r√2=2.07. After factoring, subtract 5 from 7.07 =2.07 and get √ 2 . Then solve for r=0.86. Just 2 steps

[Muslim_]

Very good
In the last splification of 'r' you can just factor out the 5 from the numerator and also you can apply the formula (a-b)(a+b) = a^2-b^2 in the denumenator

[ROCCOANDROXY]

In General, let the side of the square be r0 and beginning with the Quarter circle of radius r0 extend the diagram to an infinite number of circles tangent to each other, then we obtain

r(n) = (3 - 2 * sqrt(2))^n * r0 for each positive integer n >= 1 and the sum S of the area of all circles (including the quarter circle) is S = ((3 - sqrt(2))/(4 * sqrt(2))) * pi * r0^2.

Letting A(0) = 1/4 * pi * r0^2 implies S/A(0) = (3 - sqrt(2))/sqrt(2).

[marioalb]

Taking the square of side (R-r), we have:

r = Hypotenuse - R
r = H - R = H - 5

H² = 2 x (R-r)²

r = (2 x (R-r)²)^(1/2)- R
r + R = (2 x (R-r)²)^(1/2)
(r + R)² = 2 x (R-r)²
(r + 5)² = 2.(5-r)²
r²+10r+25 = 2.(25-10r+r²)
r²+10r+25=50-20r+2r²
r²-30r+25=0

Using the cuadratic formula:
r = 0, 858 cm. ( Solved √ )

[rodrigomarinho]

Trace a segment perpendicular to CD from point O (call the point on which the segment meets CD point E) to create the right isosceles triangle OED. Its hypothenuse is equal to r + 5 and OE is equal to 5 - r. The rest is history.

[Marina]

I figured out this task before watching the video. It's turned out that I chose the second solution.:)

[santiagoarosam]

The common tangent to both circles at point T cuts AB at point P ⇒ AP=PT ⇒ PB=(AP)√2 ⇒ AB=AP+(AP)√2=(AP)(1+√2)= 5 ⇒ AP=5(-1+√2) → If R is the sought radius ⇒ PB=AP+R ⇒ AB=2(AP)+R ⇒ R=AB-2(AP)=5–10(-1 +√2) ⇒ R=15-10√2=0.85786

[honestadministrator]

Radius of larger circle be R
Then R √2 = R + r ( √2 +1)
or r = R (√2 -1)/(√2 +1) = R (√2 -1)^2

[marioalb]

Hypotenuse = R + r + r/cos45°
H = R + r (1+1/cos45°)
r (1 + √2) = H-R
r = (H-R)/(1+√2)

R=5 cm
H²=5²+5²
H=7, 07 cm

r = (7, 07 - 5 ) / (1+√2)
r= 0.858 cm ( Solved √ )

[santiagoarosam]

Another method.- The power of point B with respect to the center circumference “D” = AB²=BT x (BD+DT) → 5²=(r+r√2)(5+5√2)] → r = 15 -10√2 = 0.85786
Cheers

[honestadministrator]

Bit of work gives
R √2 = R + r + r √2
r = R ( √2 -1) ^2

[romailto]

I guess i was using a third method )
Ratio of 5 / 5sqrt2 = r / (r + x), where x = 5sqrt2 - 5 - 2r

[batavuskoga]

I thought my solution was not correct, but I did it right. Nice explanation

[새벽달-uj]

Line DB=5√2

5√2+5:5=5√2-5:r
r=5*(5√2-5)/(5√2+5)
r=0.85786

[Patrik]

EDIT: The below soluion is incorrect, but keept as a way of approaching this problem from a different angle... THIS IS NOT A VALID SOLUTION - ITS INCOMPLETE!

talk about over complicating things....

[ here is two easier methods
its a square the angle of any of the triangles is 45, 90, 45 degrees..
Method one
se we get Diameter(X) of the circle, X is just to not comfuse with the vector point D
X = ( 5 / sin(45) ) - 5 ≈ 2.07
r = X / 2 ≈ 1.036 ...WRONG!

Method two
X = (5 * √2) - 5 ≈ 2.07
r = X /2 ≈ 1.036 ...WRONG!

Correct solution would be
X = r + r√2
r + r√2 = (5√2) - 5 ->
r(1+√2) = (5√2) - 5 ->
r=( (5|√2|) - 5)/(1+|√2|)

OR (general solution)
r = 2a * Cos(45) - a / ( 1 + Cos(45) ); a = the side of the big square



Note: √2 = 1/Cos(45) = 1/Sin(45) = 2 * Sin(45) = 2 * Cos(45)
..and therfor 5√2 is equal to 10 * Sin(45) = 10 * Cos(45) ->
a√2 = a( 2 * Sin(45) ) = a( 2 * Cos(45) ) = 2aCos(45)


...works for every rectangle
Diameter = ( sideAB / Sin(AngleADB) - SideAB;
Diameter = ( sideAD / Cos(AngleADB) - SideAD
..and the angle can be easily found using Phytagorian Theroem a^2 + b^2 = c^2 ]

..but i do think its a nice introduction to do more complex things with calculus...