filmov
tv
Learn 3 Different Methods to Find the Radius of a Circle | In-Depth Explanation
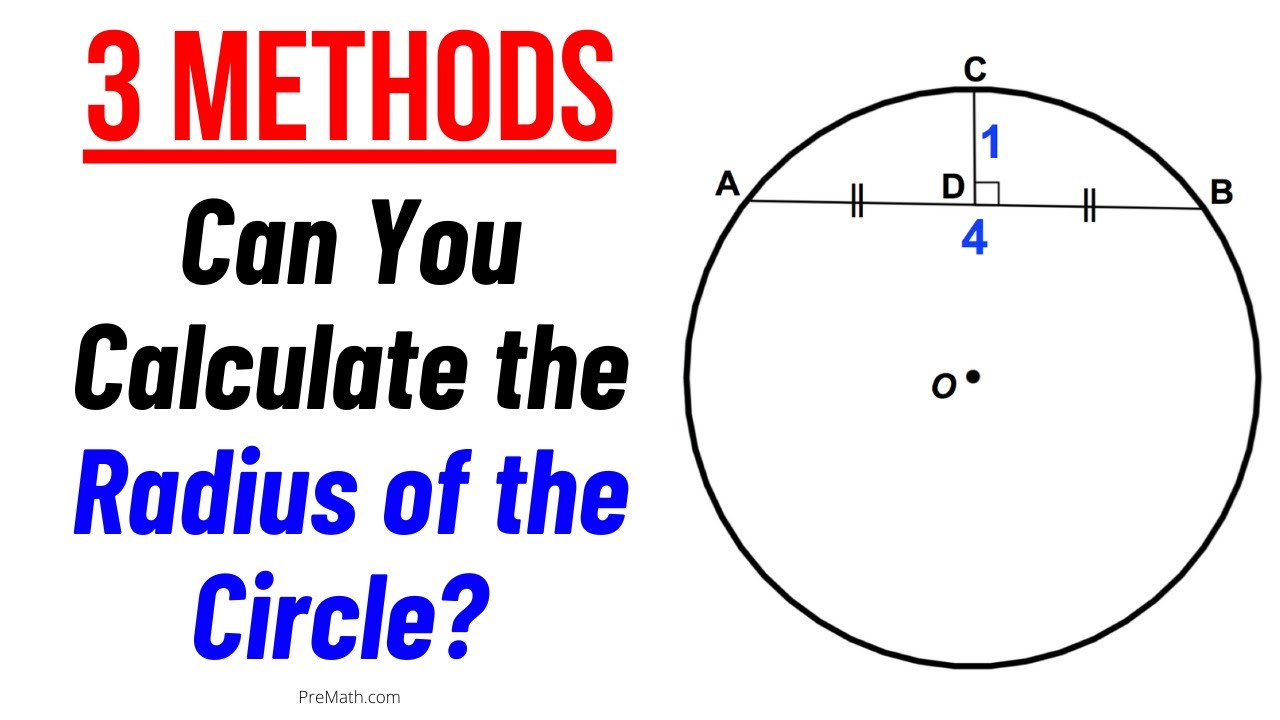
Показать описание
Learn 3 Different Methods to Find the Radius of a Circle | In-Depth Explanation
3 Different Methods for Tuning a Car [4k]
How To Learn - The 3 Main Ways
How to Solve Quadratic Equations - Using 3 Different Methods
**VERY DETAILED** How To Start A Box Braid TUTORIAL |•3 Different Methods | •BraidsbyTyTi
How to Size a Watch Bracelet (3 Different Methods) - Watch and Learn #14
All Three Spideys Learn About Each Other | Spider Man: No Way Home | With Captions
**VERY DETAILED** How To Start A Senegalese Twist TUTORIAL |•3 Different Methods | •BraidsbyTyTi
A different way to visualize rhythm - John Varney
How to strum a ukulele for beginners - 3 different methods!
Spider-Man No Way Home: All Three Spideys Learn About Each Other (HD) | With Captions
How I Take Notes for Different Subjects
The Four Personality Types and How to Deal with Them
The Best Learning Method in History: 2,400 Years Ahead of Its Time
Which car has the right of way? Understand and Resolve this common Right-of-way driving rule
How to Make Coca Cola Soda Fountain Machine with 3 Different Drinks at Home
898. How to Learn Vocabulary 📚(and not just stare at word lists) Workshop
How to Solve Quadratic Equations Using 3 Methods - Leading Coefficient Other than One
How to Tie the Truckies (Truckers) Hitch 3 Different Ways. Hitches to Secure Your Load with Rope.
How to transfer data to another sheet by vlookup #shorts #short
How to learn major parts of the brain quickly
NEW AI ANIMATION | FREE Video Generator | Different styles | Prompt Tutorial |
Learn How to Draw and Identifying the Different Types of Shapes
How to Figure Out the Key of Any Song (3 Different Methods)
Комментарии
 0:17:28
0:17:28
 0:05:46
0:05:46
 0:07:18
0:07:18
 0:09:30
0:09:30
 0:09:36
0:09:36
 0:16:09
0:16:09
 0:02:58
0:02:58
 0:11:20
0:11:20
 0:05:23
0:05:23
 0:04:32
0:04:32
 0:03:02
0:03:02
 0:05:57
0:05:57
 0:04:22
0:04:22
 0:09:51
0:09:51
 0:02:35
0:02:35
 0:03:53
0:03:53
 0:36:17
0:36:17
 0:12:52
0:12:52
 0:05:59
0:05:59
 0:00:59
0:00:59
 0:05:02
0:05:02
 0:08:03
0:08:03
 0:09:37
0:09:37
 0:06:18
0:06:18