filmov
tv
Abstract Algebra Exam 3 Review Problems and Solutions (Basic Ring Theory and Field Theory)

Показать описание
#abstractalgebra #abstractalgebrareview #ringtheory
Links and resources
===============================
(0:00) Types of problems
(0:35) Abelian groups of order 72 (isomorphism classes)
(3:20) Number of Abelian groups of order 2592 (use partitions of integer powers)
(7:02) Definition of a ring R
(11:33) Definition of a unit in a commutative ring with identity
(12:54) Definition of a zero divisor in a commutative ring
(14:56) Definition of a field F (could also define an integral domain)
(17:04) Definition of an ideal of a ring (two-sided ideal)
(19:04) Ideal Test
(20:28) Principal Ideal definition
(22:14) Principal Ideal Domain (PID) definition
(23:36) Prime Ideals, Maximal Ideals, and Factor Rings (Quotient Rings). Relationship to integral domains and fields.
(29:29) Irreducible element definition (in an integral domain)
(31:40) Z8 units and zero divisors, U(Z8) group of units
(34:09) Ring homomorphisms from Z12 to Z20
(38:38) Integral domains, fields, PIDs, UFDs, EDs (True/False)
(41:15) Z[x] is a UFD but not a PID (Z[x] is a Unique Factorization Domain but not a Principal Ideal Domain)
(42:29) Long division in Z3[x] (& synthetic division mod 3) (Division algorithm over a field)
(48:36) Reducibility test of degree 2 polynomial over field Z5
(50:43) Eisenstein's Criterion for irreducibility over the rationals Q
(52:53) Tricky factorization to prove reducibility over Q
(54:19) Mod p Irreducibility test for degree 3 polynomial over Q
(57:11) Prove fields have no nontrivial proper ideals
(1:01:21) Prove the intersection of ideals is an ideal (use the Ideal Test)
(1:05:32) Mod p Irreducibility test for degree 4 polynomial over Q
(1:12:33) Factor ring calculations in Z3[x]/A, where A is a maximal principal ideal generated by an irreducible polynomial over Z3
(1:25:12) Part of proof that Z[sqrt(-5)] is not a UFD (it's an Integral Domain that is not a Unique Factorization Domain). Need properties of a norm defined on Z[(-5)^(1/2)] and the definition of irreducible in an integral domain.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 1:33:26
1:33:26
 0:52:52
0:52:52
 1:02:42
1:02:42
 0:27:13
0:27:13
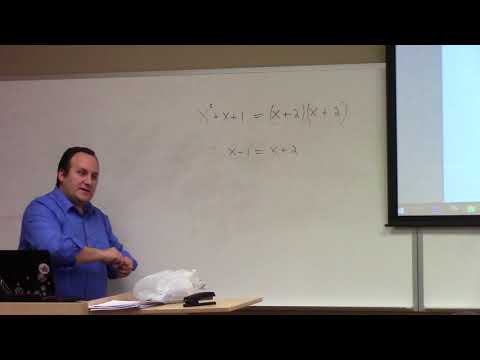 0:47:33
0:47:33
 1:30:20
1:30:20
 0:30:24
0:30:24
 0:01:00
0:01:00
 1:22:00
1:22:00
 1:18:42
1:18:42
 0:02:14
0:02:14
 0:04:03
0:04:03
 0:44:27
0:44:27
 0:00:37
0:00:37
 0:00:29
0:00:29
 0:00:15
0:00:15
 0:00:16
0:00:16
 0:59:51
0:59:51
 0:00:15
0:00:15
 0:31:28
0:31:28
 1:04:52
1:04:52
 0:08:50
0:08:50
 0:05:21
0:05:21
 0:00:50
0:00:50