filmov
tv
ONLY 3 Students Passed?! This Hard Abstract Algebra Exam made 96% of Math Students FAIL!

Показать описание
Today we take a look at yet another university exam where nearly all students failed! This time, it's an abstract algebra and arithmetic exam, that revolves around Group, ring and field theory, matrix diagonalization and elementary number theory. Enjoy! =D
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
ONLY 3 Students Passed?! This Hard Abstract Algebra Exam made 96% of Math Students FAIL!
Only 3% pass this Brazilian exam
ONLY 3% Of People Can Pass This Selective Attention Test - Focus Carefully..👁
Worst Ways People Have ALMOST Died 😱 (Part 3) #ytshorts
Only clowns at 3 AM will pass this #clowns #halloween #horrorshorts
Noise Colorfit Vision 3 Display🔥Fire Durability Test Watch Pass #shorts #video #short #test #viral...
Tense 3 Form | Present, Past, Participle | Part 6
Only 3 In 10 People Can Pass This IQ Riddle Quiz!
We're passing the phone to 3 hilarious Cooper kids... #YoungSheldon
Strangest ways people have died… (Part 3) #shorts #youtubeshorts
3 TIPS for LONG PASS!!🦵⚽️#football #soccer #shorts
Bro died 3 times for just a bowl of rice #edit #onepiece #luffy #zoro #music #animeedit #shorts
Ranking Every Chapter 4 Season 3 Battle Pass Skin In Fortnite
3-Person Pass, Cut, & Replace
Only 1% Can Pass The Healthy Lungs Test LEVEL 3 🫁😳
Why People FAIL Calculus (Fix These 3 Things to Pass)
BSL level 3 pass! 🥳 | BSL only - no captions | #britishsignlanguage #bslstudent #signlanguage
Easily 3 Star Dungeons & [Clash of] Dragons Challenge (Clash of Clans)
Only 3% of People Can Pass all These Optical illusions😵💫⏱
Kung Fu Panda 3 - Passing the Torch - Scene with Score Only
Door to the past (Poppy Playtime 3 Animation)
Fast ASMR ONLY 3% Will Pass Doctor Cranial Nerve Exam Roleplay #shorts
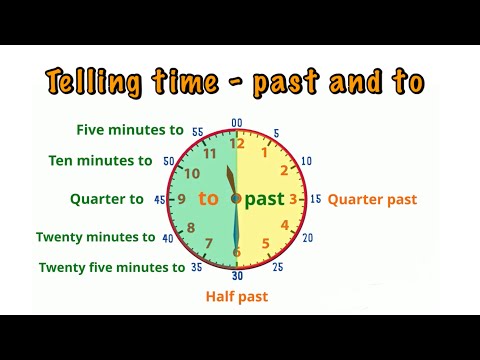
Telling time (4)- the minutes- past and to- grade 3- grade 4
Splatoon 3: Expansion Pass - Side Order DLC – Mobility color chips
Комментарии
 0:27:13
0:27:13
 0:14:02
0:14:02
 0:00:23
0:00:23
 0:00:22
0:00:22
 0:00:16
0:00:16
 0:00:13
0:00:13
 0:00:16
0:00:16
 0:14:09
0:14:09
 0:00:26
0:00:26
 0:00:29
0:00:29
 0:00:22
0:00:22
 0:00:49
0:00:49
 0:00:56
0:00:56
 0:02:15
0:02:15
 0:01:06
0:01:06
 0:03:15
0:03:15
 0:00:31
0:00:31
 0:03:30
0:03:30
 0:00:57
0:00:57
 0:04:14
0:04:14
 0:00:21
0:00:21
 0:01:00
0:01:00
 0:03:46
0:03:46
 0:00:44
0:00:44