filmov
tv
Linear Algebra 4b: Impossible Decomposition with Polynomials

Показать описание
Linear Algebra 4b: Impossible Decomposition with Polynomials
Linear Algebra 4a: Impossible Decomposition with Geometric Vectors
Linear Algebra 4c: Impossible Decomposition in ℝⁿ
Linear Algebra 4d1: A Property Irrelevant in Decomposition Problems
Linear Algebra 3e: Linear Systems Are a Decomposition Problem
Linear Algebra 3b4: Decomposition with Respect to Arbitrary Geometric Vectors, Affine Grid
UPSC VS IIT JEE 🥵 #iitstatus #motivation #toppers #iitjee #jeemains #upscstatus #neet #nit #jee
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
WHY I HATE MATH 😭 #Shorts
Linear Algebra 3b2: Decomposition with Geometric Vectors 2
Linear Algebra 3d3: Decomposition in ℝⁿ, 3
Linear Algebra 3c1: Decomposition with Polynomials 1
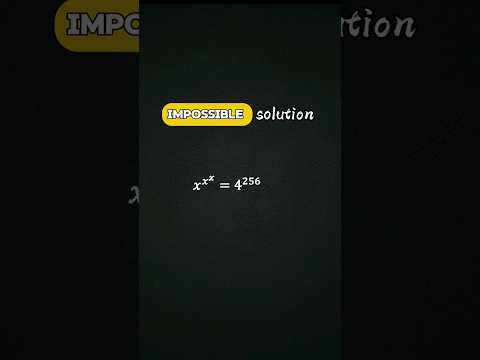
This Equation Had Me Stumped... But Don't Worry, I Got You!#maths
LU decomposition & LDU decomposition using Elementary Row Operations | Linear Algebra
Maths vs Physics
Linear Algebra 3d2: Decomposition in ℝⁿ, 2
Linear Algebra 3c2: Decomposition with Polynomials 2
Linear Decomposition
Linear Algebra 3b1: Decomposition with Geometric Vectors 1
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
LU Decomposition Example | Numerical Methods
Prime Decomposition Is the Key
Visualize Spectral Decomposition | SEE Matrix, Chapter 2
Linear Algebra 3d1: Decomposition in ℝⁿ 1
Комментарии
 0:09:49
0:09:49
 0:07:13
0:07:13
 0:08:56
0:08:56
 0:02:57
0:02:57
 0:09:06
0:09:06
 0:13:29
0:13:29
 0:00:14
0:00:14
 0:00:15
0:00:15
 0:00:24
0:00:24
 0:09:28
0:09:28
 0:06:52
0:06:52
 0:05:29
0:05:29
 0:00:24
0:00:24
 0:11:37
0:11:37
 0:00:25
0:00:25
 0:06:17
0:06:17
 0:11:05
0:11:05
 0:03:02
0:03:02
 0:11:28
0:11:28
 0:12:09
0:12:09
 0:04:47
0:04:47
 0:04:25
0:04:25
 0:15:55
0:15:55
 0:05:04
0:05:04