filmov
tv
Solve xy'+2y=x+2, Domains of Validity
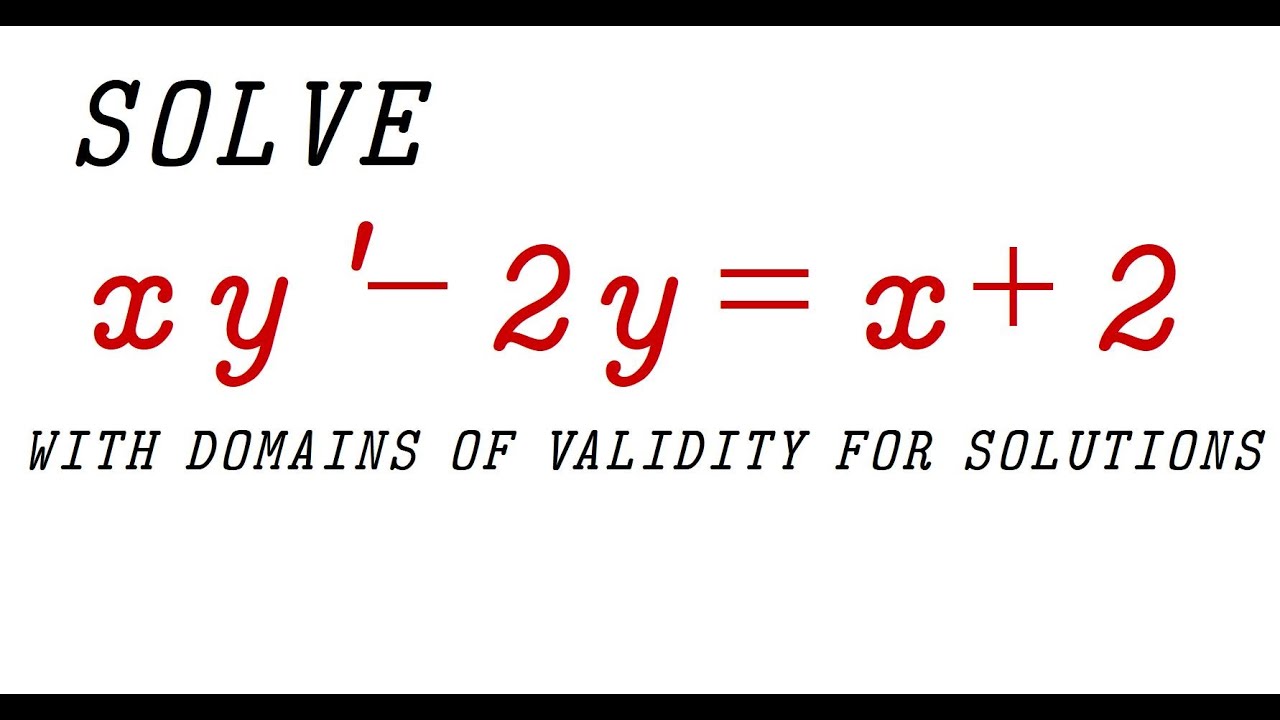
Показать описание
In this video, we will solve the differential equation xy' + 2y = x + 2. First, divide each term by x, resulting in y' + 2y/x = 1 + 2/x. Notice that 2/x is undefined at x = 0, so keep that in mind. Identify the integrating factor, which is e^(2ln|x|) = |x|^2. Multiply each term by x^2 to get the equation 2xy + x^2 = x^2 + 2x. Simplify further to obtain x^2y' = 2x. Integrate both sides to get x^2y = (1/3)x^3 + x^2 + c. Divide each term by x^2 to isolate y, giving y = (1/3)x + 1 + c/x^2.
Exercise 1
Solve the initial value problem y(0) = 1.
Solution
Substitute x = 0 and y = 1 into the general solution. 1 = (1/3)(0) + 1 + c/(0)^2. Since the term c/(0)^2 is undefined, this initial value problem does not have a solution.
Exercise 2
Solve the initial value problem y(-3) = 0.
Solution
Substitute x = -3 and y = 0 into the general solution. 0 = (1/3)(-3) + 1 + c/(-3)^2. Simplifying this equation gives c = 0. Therefore, the solution to this initial value problem is y = (1/3)x + 1.
Exercise 3
Find the domain of validity for the solution y = (1/3)x + 1 + c/x^2.
Solution
The domain of validity depends on the value of c. If c = 0, then the solution is valid for all real numbers except x = 0. If c ≠ 0, the solution has a vertical asymptote at x = 0, and it is valid for x 0 and x 0.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
Exercise 1
Solve the initial value problem y(0) = 1.
Solution
Substitute x = 0 and y = 1 into the general solution. 1 = (1/3)(0) + 1 + c/(0)^2. Since the term c/(0)^2 is undefined, this initial value problem does not have a solution.
Exercise 2
Solve the initial value problem y(-3) = 0.
Solution
Substitute x = -3 and y = 0 into the general solution. 0 = (1/3)(-3) + 1 + c/(-3)^2. Simplifying this equation gives c = 0. Therefore, the solution to this initial value problem is y = (1/3)x + 1.
Exercise 3
Find the domain of validity for the solution y = (1/3)x + 1 + c/x^2.
Solution
The domain of validity depends on the value of c. If c = 0, then the solution is valid for all real numbers except x = 0. If c ≠ 0, the solution has a vertical asymptote at x = 0, and it is valid for x 0 and x 0.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
 0:05:39
0:05:39
 0:03:03
0:03:03
 0:00:25
0:00:25
 0:05:52
0:05:52
 0:03:21
0:03:21
 0:00:11
0:00:11
 0:00:14
0:00:14
 0:00:11
0:00:11
 0:01:43
0:01:43
 0:07:23
0:07:23
 0:08:57
0:08:57
 0:00:29
0:00:29
 0:00:11
0:00:11
 0:02:21
0:02:21
 0:00:20
0:00:20
 0:00:16
0:00:16
 0:00:11
0:00:11
 0:00:16
0:00:16
 0:00:14
0:00:14
 0:00:20
0:00:20
 0:05:22
0:05:22
 0:00:11
0:00:11
 0:02:46
0:02:46
 0:00:52
0:00:52