filmov
tv
What is the limit of sin (1/x)? - Week 1 - Lecture 8 - Mooculus

Показать описание
Calculus - The limit of a function
Limits and Limit Laws in Calculus
Calculus - The limit of a function basics
Infinite Limit Shortcut!! (Calculus)
Limits in Calculus: Definition & Meaning. What is a Limit?
Definition of the Limit of a Sequence | Real Analysis
Solving limits by factoring | Calculus Tutorial and Help
What is a Limit - What is a Derivative , Calculus 1 , Lesson 1
AP Calculus AB/BC | Topic 1.2 & 1.4 | Defining Limits + Estimating from Tables
How To Find The Limit At Infinity
Limits | Finding the limit of an infinite series
This is a very famous limit
But what is the Central Limit Theorem?
2. what is Limit (Hindi) |
proving the limit of a product is the product of the limits, epsilon-delta definition
Limit of Function (part 1) - Calculus and Analytic Geometry
Mark Ambor - Sky is the Limit (Official Lyric Video)
#limit # how to solve of limits in trigonometric identities, limit x→0, sinx,e²-1/x,x/tanx
How To Tell If The Limit Exists
The Limit On Einstein's General Theory Of Relativity 🤯 w/ Neil deGrasse Tyson
What is a Limit in Calculus? – a very basic introduction
The precise definition of the limit EXPLAINED! (KristaKingMath)
❖ Finding the Limit of a Sequence, 3 more examples ❖
What is the limit of speed? 1,000 km/h car! #funny
Комментарии
 0:04:56
0:04:56
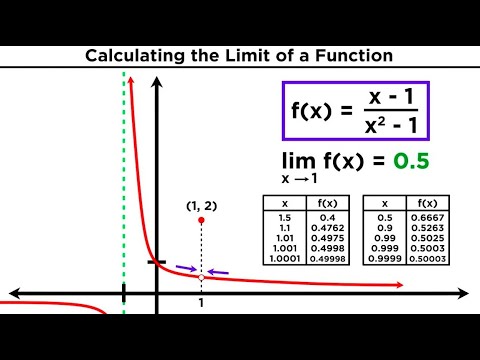 0:12:49
0:12:49
 0:02:26
0:02:26
 0:00:51
0:00:51
 0:17:16
0:17:16
 0:13:59
0:13:59
 0:00:42
0:00:42
 0:04:40
0:04:40
 0:10:52
0:10:52
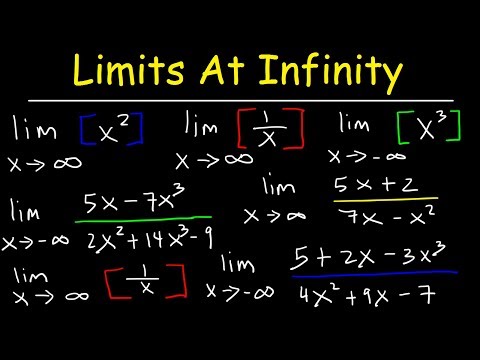 0:13:14
0:13:14
 0:03:17
0:03:17
 0:00:48
0:00:48
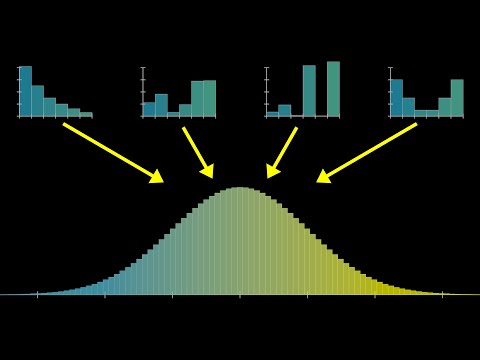 0:31:15
0:31:15
 0:05:57
0:05:57
 0:28:27
0:28:27
 0:14:08
0:14:08
 0:02:40
0:02:40
 0:00:07
0:00:07
 0:09:22
0:09:22
 0:00:37
0:00:37
 0:18:50
0:18:50
 0:11:28
0:11:28
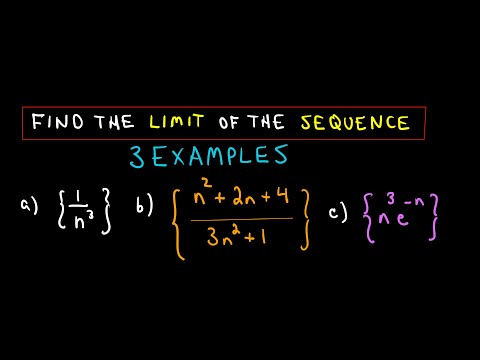 0:03:24
0:03:24
 0:00:32
0:00:32