filmov
tv
Sum of the first n natural numbers, 3 simples ways

Показать описание
1+2+3+...+n,
blackpenredpen,
math for fun,
blackpenredpen,
math for fun,
Find the sum of first n squares, difference equation approach, (ft. Max!)
Sum of first n odd numbers | Visual mathematics |
Sum of the first n odd numbers (visual proof)
Sum of the first n natural numbers, 3 simples ways
Sum of first n cubes - Mathematical Induction
The Sum of the First N Odd Numbers | Visual Proof
Sum of the first n natural numbers, Combinatoric, difference Equation
Sum Of The First N Natural Numbers | Python Example
Sum of the First N Terms of an Arithmetic Sequence
Sum of first 'n' terms of an Arithmetic Progression | Part 1/3 | English | Class 10
Principle of Mathematical Induction The Sum of the First n Integers Proof
Sum of the k^th Powers of the First n Positive Integers
How to Sum of the First N Positive Integers in Python
Proof of the formula for the sum of the first n integers without Induction
Sum Of Cubes I (visual proof)
Sum of the first n Natural Numbers || Maths Activity / Project / TLM
Sum The First N Natural Numbers Using Recursion | C Programming Example
Find the sum of first n Even Natural Numbers Formula
If the sum of the first n terms of an Ap is 4n-n2 what is first term? what is the sum of first two
05.07 Ex2 Prove sum of first n odd numbers is n^2 by induction
Sum of n squares | explained visually |
SUM OF ARITHMETIC PROGRESSION (A.P)
Sum of First n Natural Numbers Derivation - Sequence and Series - Maths Class 11
Arithmetic Series - Sum of the Terms of Arithmetic Sequence
Комментарии
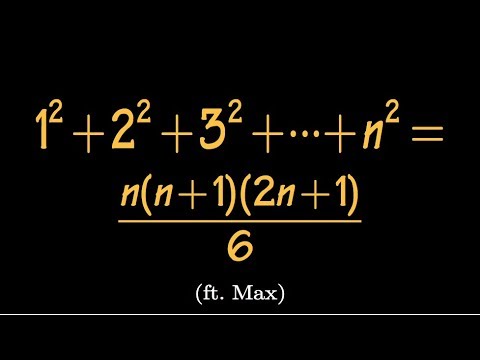 0:11:19
0:11:19
 0:01:26
0:01:26
 0:01:27
0:01:27
 0:13:55
0:13:55
 0:12:34
0:12:34
 0:01:41
0:01:41
 0:19:43
0:19:43
 0:04:47
0:04:47
 0:03:49
0:03:49
 0:04:58
0:04:58
 0:04:45
0:04:45
 0:10:49
0:10:49
 0:01:14
0:01:14
 0:01:45
0:01:45
 0:01:38
0:01:38
 0:05:31
0:05:31
 0:05:10
0:05:10
 0:06:09
0:06:09
 0:05:57
0:05:57
 0:02:32
0:02:32
 0:02:14
0:02:14
 0:04:50
0:04:50
 0:06:03
0:06:03
 0:09:06
0:09:06