filmov
tv
Sum of first n cubes - Mathematical Induction

Показать описание
In this video, I prove that the sum of the first n cubes is the square of the sum of the first n natural numbers
Sum of first n cubes - Mathematical Induction
Sum Of Cubes I (visual proof)
Sum of cubes of first n natural numbers #maths #themathprofessor #video
Visual Proof for the Sum of the First n Cubes
Prove by induction, Sum of the first n cubes, 1^3+2^3+3^3+...+n^3
Sum of First N Cubes Equals Square of 1+2+3+...+n | Number Theory
100 Subscriber Special: The sum of the first n cubes (proof by Induction)
The method of differences and sum of cubes of natural numbers
Find the sum of first n squares, difference equation approach, (ft. Max!)
Sum of First n Cubes (Algebraic and Visual Proof)
Sum of cubes of first n natural numbers | Class 11 Chapter 9 NCERT | e-Vidyalaya
Sum of cubes of the first 'n' natural numbers
Proof of sum of cubes of the first n natural numbers
Sum of the Cubes of 'n' Consecutive integers - Simple Proof
Sum of first n cubes
Geometrical Way To Prove The Sum of Cubes of First 'n' Natural Numbers | PJ Exclusive |Pra...
Sum of Cubes of First n Natural Numbers Derivation - Sequence and Series - Maths Class 11
Sum of cubes of the first n odd numbers
Summing cubes without words #phonk #phonkmath
# square root of sum of the cubes of first 'n' natural numbers//....
proof of Sum of cubes of first n natural numbers by mathematical induction
232.Sum of Squares and Cubes of first n Natural Numbers 232
Trick | Sum of Cubes | First 'n' Natural Numbers | Natural Number Series - By ZOHEB SIR
Derivation | Formula | Sum of first n squares or square numbers 1^2 + 2^2 + 3^2 + 4^2 +...n^2
Комментарии
 0:12:34
0:12:34
 0:01:38
0:01:38
 0:02:41
0:02:41
 0:01:40
0:01:40
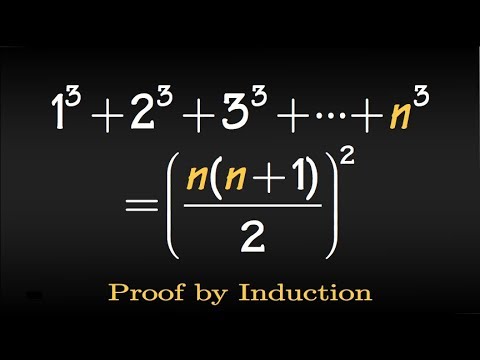 0:09:03
0:09:03
 0:11:59
0:11:59
 0:09:51
0:09:51
 0:03:59
0:03:59
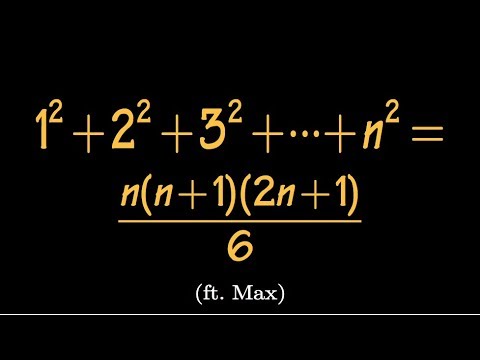 0:11:19
0:11:19
 0:02:51
0:02:51
 0:09:29
0:09:29
 0:04:53
0:04:53
 0:15:17
0:15:17
 0:12:23
0:12:23
 0:00:58
0:00:58
 0:06:50
0:06:50
 0:13:05
0:13:05
 0:12:30
0:12:30
 0:00:26
0:00:26
 0:04:20
0:04:20
 0:05:57
0:05:57
 0:08:43
0:08:43
 0:06:35
0:06:35
 0:05:30
0:05:30