filmov
tv
Solving a Russian Math Olympiad Problem | Solve for x If 4^27 + 4^1000 + 4^x is a Perfect Square

Показать описание
🔴Solving a Russian Math Olympiad Problem | Solve for the Largest x for Which 4^27 + 4^1000 + 4^x would be a Perfect Square |
Hey there.
Today, we are dealing with a nice Russian Math Olympiad problem, in which we want to solve for the largest integer x, such that 4^27 + 4^1000 + 4^x would be a perfect square. Now finding an integer that will make 4^27 + 4^1000 + 4^x a perfect square, is not really hard, but the tricky part of this question is that we don't know if the x we find is the largest x possible or not.
So in order to solve this interesting Russian Math Olympiad question, we will find a value for x, and then we will try to find out if there is a larger value for x or not.
🔴I hope you enjoy watching this video on a really nice Russian Math Olympiad problem .🔴
Don't forget to:
✅ Leave a comment
✅ Subscribe
✅ Hit the like button
✅ Ring the bell
topics covered in this video:
Prove that this expression is a perfect square
solve for x
solving a nice math olympiad problem
solving a Russian math olympiad problem
how to solve for x if 4^27 + 4^1000 + 4^x is a perfect square
#SolveForX #RussianMathOlympiad #matholympiad #AnonMath #QuadraticEquation #matholympiadquestion
Комментарии
 0:08:01
0:08:01
 0:03:42
0:03:42
 0:20:56
0:20:56
 0:09:35
0:09:35
 0:07:27
0:07:27
 0:03:33
0:03:33
 0:10:40
0:10:40
 0:12:16
0:12:16
 0:07:10
0:07:10
 0:27:41
0:27:41
 0:03:58
0:03:58
 0:02:12
0:02:12
 0:02:34
0:02:34
 0:10:45
0:10:45
 0:02:29
0:02:29
 0:02:51
0:02:51
 0:08:26
0:08:26
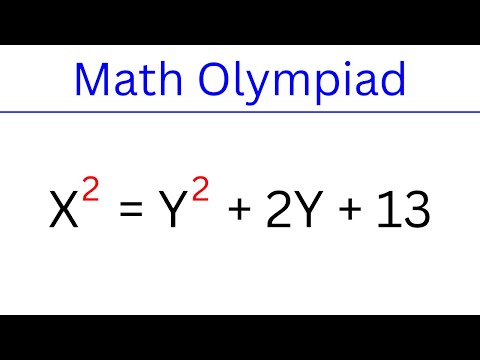 0:23:29
0:23:29
 0:03:57
0:03:57
 0:02:35
0:02:35
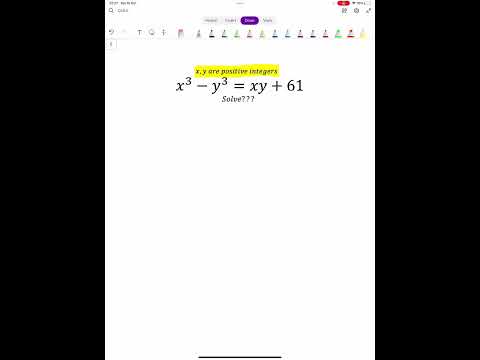 0:00:12
0:00:12
 0:03:00
0:03:00
 0:05:33
0:05:33
 0:02:43
0:02:43