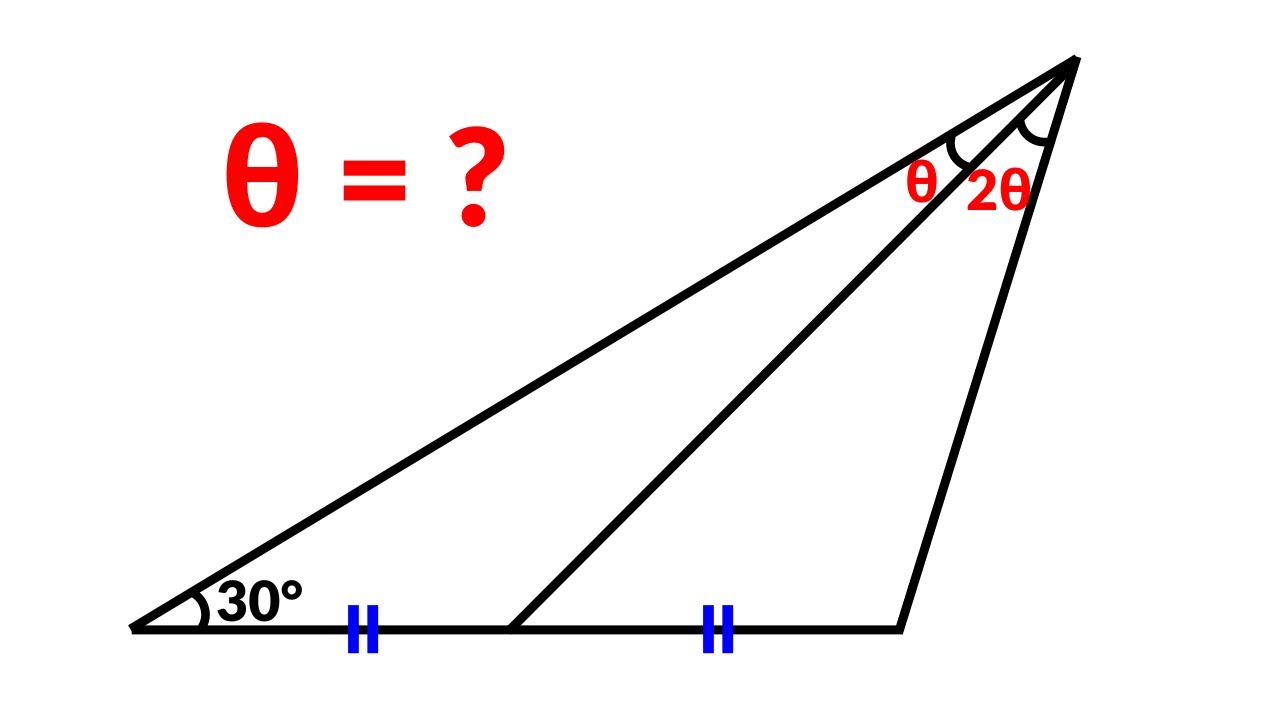
China Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods

GET MY EBOOKS
•••••••••••••••••••••••

OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------

Join the channel to become a member

[jimlocke]

Extend BC to the right and drop a perpendicular from A to the extension. Label the point of intersection as point E. Without loss of generality, we can let length AE = 1. Let length BD = CD = m and length CE = n. By sum of angles of a triangle = 180°, we get <BAE = 60°. <CAE = <BAE - 3Θ = 60° - 3Θ. So, tan(60° - 3Θ) = n, tan(60° - Θ) = m + n, tan(60°) = 2m + n. We know that tan(60°) = √(3)/2, so 2m + n = √(3) and n = √(3) - 2m. So, we eliminate variable n. We can use the tangent difference of angles formula to solve for tan(Θ) and tan(3Θ). That formula is tan(α - ß) = (tan(α) - tan(ß))/(1 + tan(α)tan(ß)). In the first case, let α = 60° and ß = Θ. In the second case, let α = 60° and ß = 3Θ. We can compute tan(2Θ) from tan(Θ) by the tangent double angle formula. Then, we have tan(3Θ) = tan(2Θ + Θ) and have a formula which can be solved for m. We compute n from n = √(3) - 2m and take arctan(n), which equals 60° - 3Θ, which we solve for Θ.

We can always take an educated guess that <CAE = 15°, then Θ = 15°. n = tan(15°) = 2 - √(3) = √(3) - 2m, 2m = 2√(3) - 2. m = √(3) - 1 DE = m + n = √(3) - 1 + 2 - √(3) = 1. So, tan(<DAE) = 1 and <DAE = 45°, so 45° = 2Θ + 15° and Θ = 15°. If Θ = 15°, <BAE is correctly 60°. As a final check, tan(<BAE) = 2m + n = 2√(3) - 2 + 2 + √3 = √(3) and tan(60°) = √(3).

[oscarcastaneda]

Construct the semicircle with diameter BC and center D.

It can be shown that the foot of the height from C to AB is split into 30 deg and 60 deg by the radius of the semicircle, which satisfies the condition of the problem statement.

Hence, theta can also be 30 deg.

[holyshit]

sine law gives two results
theta = 30 and theta = 15
x/sin(theta) = y/sin(150-theta)
2x/sin(3theta) = y/sin(150-3theta)
x/y = sin(theta)/sin(150-theta)
2x/y = sin(3theta)/sin(150-3theta)
And we have followinng equation
sin(3theta)/sin(150-3theta) - 2sin(theta)/sin(150-theta) = 0
This equation can be reduced to the polynomial equation of third degree in terms of tan(theta)

[michaeldoerr]

The angle theta is 15°. This problem is REALLY similar to the other problems and I am starting to think that the angle 15° should be understood as an essential angle that regardless of method should be expected. Also I commented on yesterday's video and I FINALLY got the HL similarity right!!!

[purnajinananandaavadhuta]

Two methods are entirely different and it is marvelous.

[elroqxu]

Use wildfire creo to draw a circle. A straight line passes through the center of the circle. Take the center of the circle and two points on the circle. Mark 30 degrees. sd1=2*sd2. There are many results.

[ДмитрийИвашкевич-ят]

Площади треугольников ABD и DBC равны: S(ABD)=S(DBC)
AB*BD*sinα=BD*BC*sin2α
AB=2*BC*cosα
Пусть h высота треугольника ABC, тогда h=AB*sin30°=AB/2=BC*cosα
В случае если угол ACB>90°:
α+2α+α=60°
α=15°
Если допустить, что угол ACB<90°, то cos(3α-60°)=cosα
α=30°

[uferbenzo]

second result : teta =30 6:49 because (90-teta+30+3*teta=180 >> teta =30)

[teoremaferma]

Задача имеет два решения : одно приведено ( излишне сложно ), другое почти очевидное, если угол BAC прямой.

[arizonarunner]

There are two solutions to this problem. One solution is Θ = 30° which forms △ ABC 30°-60°-90°. Another solution is Θ = 15° which forms △ ABC 30°-45°-105°.
The end result of solving gave this equation: 64*sin⁶(Θ) - 80*sin⁴(Θ) + 20*sin²(Θ) - 1 = 0 (square root of cubic equation). I also used FreeCAD drawing to prove.

[quigonkenny]

As ∠ABC = 30° and ∠CAB = θ+ 2θ = 3θ, ∠BCA = 180°-(30°+3θ) = 150°-3θ. Let BC = DC = x.

By the law of sines:

Triangle ∆BDA:
DA/sin(30°) = BD/sin(θ)
DA/BD = sin(30°)/sin(θ)
DA/x = 1/2sin(θ)

Triangle ∆DCA:
DA/sin(150°-3θ) = DC/sin(2θ)
DA/DC = sin(150°-3θ)/sin(2θ)
DA/x = sin(30°+3θ)/2sin(θ)cos(θ)

1/2sin(θ) = sin(30°+3θ)/2sin(θ)cos(θ)
1 = sin(30°+3θ)/cos(θ)
cos(θ) = sin(30°+3θ)
sin(90°-θ) = sin(30°+3θ)
90° - θ = 30° + 3θ
4θ = 90° - 30° = 60°
θ = 60°/4 = 15°

Edit: In your second method, you can avoid the more complex equation regarding triangle ∆CDF by recognizing that ∆CDF and ∆FAD are similar triangles. Thus the 60°-2θ in ∆CDF equals the 2θ in ∆FAD, from which the solution of 15° can be easily found.

[murdock]

φ=30° → sin⁡(3φ) = 1; ∆ ABC → AB = AP + BP; BC = BD + CD = a + a; ABC = φ
DAB = θ; CAD = 2θ → θ = ? BD = PD = a → PBD = DPB = φ → PDC = DCP = 2φ → CPD = 2φ
PD = PA = a → APD = 5φ → PDA = DAP = φ/2 = θ; btw: AC = a√2; AD = (a√2/2)(√3 + 1)

[ناصريناصر-سب]

When solving the equation sin(90-θ)=sin(30+3θ), there is a case that the solution did not address, which is 90-θ+30+3θ=180, and from it θ=30. In this case, the triangle ABC is right at A.

[shaozheang]

i thought of constructing triangle ACE where angle AEC is 90. There would be 30 60 90 special triangle

[teoremaferma]

Тригонометрическое уравнение имеет два решения: 15 и 30 гр.

[prossvay]

Delta=15° (according to theorem sinus)

[RealQinnMalloryu]

{150°BAD+30°DCA}/180°BADDCA 3^60 3^30^2 3^3^10^2 1^3^2^5^2 3^1^1^2 32 (BADDCA ➖ 3BADDCA+2).

[giuseppemalaguti]

Col teorema dei seni risulta 2cosθ=cos3θ+√3sin3θ...da cui risulta θ=30(uhm..), θ=15

[georgexomeritakis]

The problem has 2 solutions: theta = 15 or 30 degrees.