filmov
tv
Comparing (sqrt(6)+sqrt(2))/2 and 5pi/6
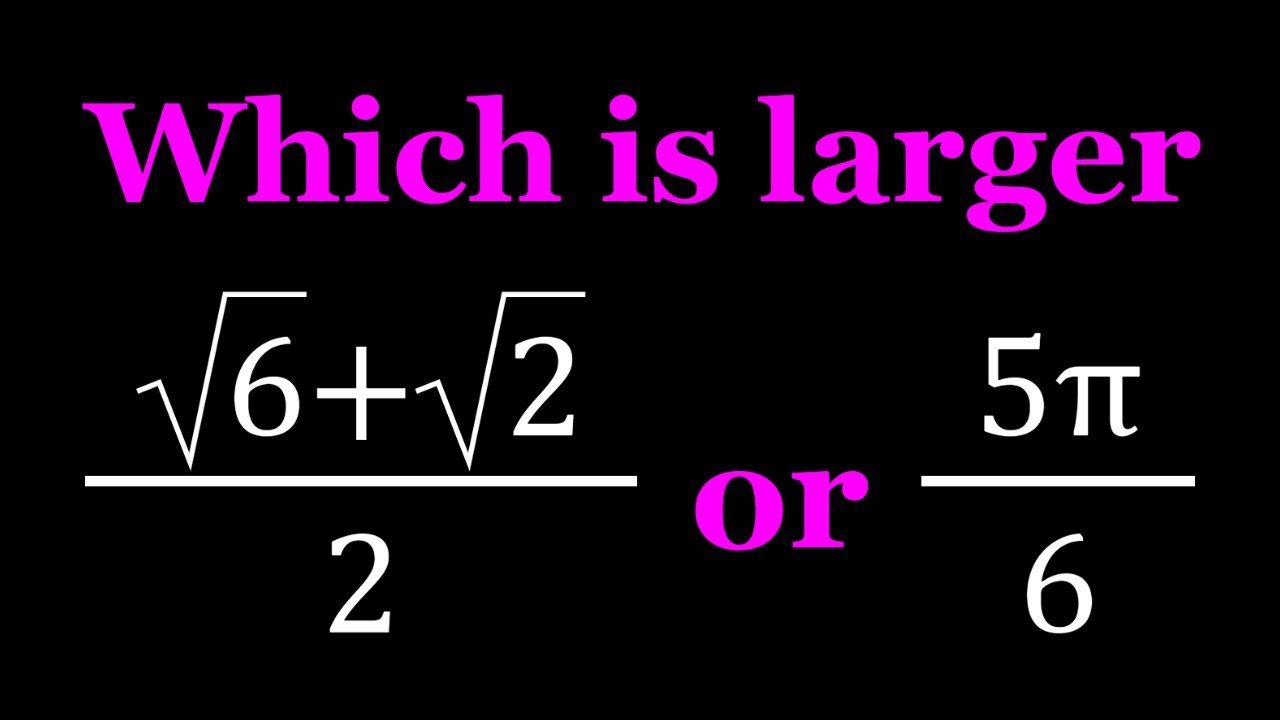
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#comparingnumbers #radicals #trigonometry
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#comparingnumbers #radicals #trigonometry
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Comparing (sqrt(6)+sqrt(2))/2 and 5pi/6
Solving an Interesting Exponential Equation
A Nice Rational Equation | #algebra
IIT Bombay CSE 😍 #shorts #iit #iitbombay
An Exponential Equation with Logs | Surprising Results
A Radical Exponential Equation | Bonus at the End
Evaluating Inverse Trigonometric Functions
Simplifying a Quick and Easy Trigonometric Expression
Unizor - Trigonometry - Lim (SIN(x)/x)
A Cubic Equation with Radicals | #polynomials
Radians and Degrees
Tough times Never last 😊✌️ #delhipolice #motivation
How To Use Reference Angles to Evaluate Trigonometric Functions
A Differential Equation from Jee Advanced | #calculus
Comparing e and 65/24
Can You Simplify a Trigonometric Expression? | Two Methods
A Ratio Problem with Radicals
SEE optional math (Trigonometry) - episode 21 (Bikram sir)
Product of sines
The Pi Song 3.0 (Memorize 300 Digits Of π)
Week 1 - Lecture 5
Problems - Definite integrals 6
The greatest among `(sin1+cos1)`, `(sqrt(sin1)+sqrt(cos1))`, `(sin1-cos1)` and 1 is
Identities Rewrite so not a fraction
Комментарии
 0:08:51
0:08:51
 0:08:45
0:08:45
 0:09:32
0:09:32
 0:00:11
0:00:11
 0:10:44
0:10:44
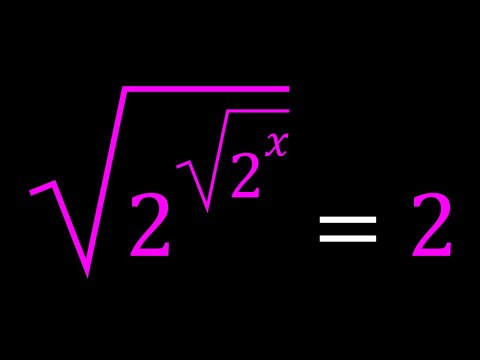 0:05:05
0:05:05
 0:22:47
0:22:47
 0:04:33
0:04:33
 0:19:44
0:19:44
 0:09:53
0:09:53
 0:18:55
0:18:55
 0:00:22
0:00:22
 0:10:59
0:10:59
 0:09:16
0:09:16
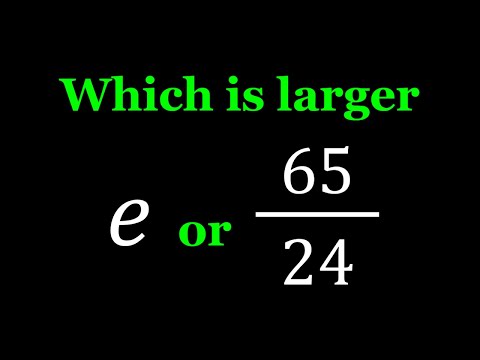 0:10:16
0:10:16
 0:05:45
0:05:45
 0:08:57
0:08:57
 0:09:38
0:09:38
 0:32:31
0:32:31
 0:04:19
0:04:19
 0:29:19
0:29:19
 0:02:32
0:02:32
 0:03:44
0:03:44
 0:02:02
0:02:02