filmov
tv
Prove that (3n+1)7^n - 1 is divisible by 9 (Mathematical Induction)

Показать описание
Prove that (3n+1)7^n - 1 is divisible by 9 (Mathematical Induction)
Prove by the principle of Mathematical induction |1/1.4 + 1/4.7 + 1/7.10 + … + 1/(3n-2)(3n+1)=n/3n+1...
Prove 3^(2n+1) + 2^(n-1) is divisible by 7 using Mathematical Induction
Proving Divisibility Statement using Mathematical Induction (1)
Mathematical Induction: Prove that 1/1.4 + 1/4.7 + 1/7.10 ... + 1/(3 n-2)(3 n+1) = n/(3 n+1)
Induction Divisibility
Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis
010 - Inductive Proof - Example 1 (1 + 4 + 7 + … + (3n – 2) = n(3n – 1) by 2) | TOC by Mahesh Goyani...
Prove that `{2^(3n) -7 n-1}` is completely divisible by the number 49
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Mathematical Induction - Divisibility Tests (1) | ExamSolutions
Show that 1/1.4+1/4.7+...+n terms=n/3n+1 || Mathematical induction || P1
MATHEMATICAL INDUCTION | Q_5 | EDUTAINMENT ONLINE
Maths Proof - Prove That (3n+1)^2-(3n-1)^2 Is Always A Multiple Of 12,For All Positive Integers Of n
Prove by the principle of Mathematical induction |1/3.5 + 1/5.7 + 1/7.9 +…+ 1/(2n+1)(2n+3)=n/3(2n+3)...
maths trick | 2^3n-7n-1 id divisible by #binomialtheorem #maths
Direct Math Proof: If n is odd then 3n + 7 is even
1/1.4 + 1/4.7 + 1/7.10 +....upto n terms = n/3n+1 @EAG
Prove that (1 + 3/1) (1 + 5/4) (1 + 7/9) ..... (1 + 2n+1/n^2) = (n + 1)^2
Prove by the principle of mathematical induction that for all `n in N` : `1+4+7++(3n-2)=1/2n(3n-1)`
Prove that 3^n-1 is divisible by 2 for all positive integers. Mathematical Induction
1+4+7+...+(3n-2)= n(3n-1)/2 by Mathematical induction
Proof by Mathematical Induction | Part 3 | Pre-Calculus
Prove that 8^n-1 is divisible by 7 for all positive integers. Mathematical Induction
Комментарии
 0:10:48
0:10:48
 0:11:15
0:11:15
 0:05:07
0:05:07
 0:06:25
0:06:25
 0:08:31
0:08:31
 0:20:35
0:20:35
 0:06:53
0:06:53
 0:05:50
0:05:50
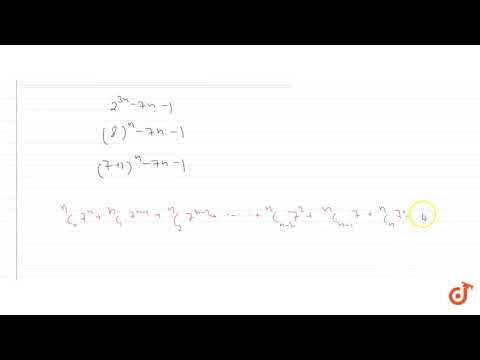 0:02:57
0:02:57
 0:22:09
0:22:09
 0:08:35
0:08:35
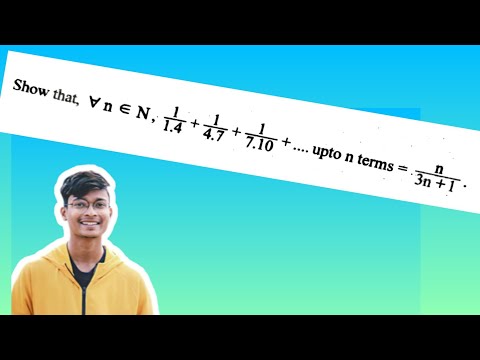 0:16:07
0:16:07
 0:06:28
0:06:28
 0:02:50
0:02:50
 0:13:12
0:13:12
 0:00:57
0:00:57
 0:04:48
0:04:48
 0:17:41
0:17:41
 0:09:24
0:09:24
 0:03:51
0:03:51
 0:03:53
0:03:53
 0:04:44
0:04:44
 0:12:38
0:12:38
 0:04:44
0:04:44