filmov
tv
Direct Math Proof: If n is odd then 3n + 7 is even

Показать описание
In this video I prove that if n is an odd integer then 3n + 7 is an even integer. This is a good proof for learning proof structure.
(the above links are my affiliate links)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
(the above links are my affiliate links)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Direct Math Proof: If n is odd then 3n + 7 is even
Discrete Math - 1.7.1 Direct Proof
Discrete Math Proofs in 22 Minutes (5 Types, 9 Examples)
[Discrete Mathematics] Direct Proofs Examples
How to Prove Math Theorems | 1st Ex: Even + Odd = Odd
Proof by Contradiction | Method & First Example
Proof by Contrapositive | Method & First Example
Discrete Math 1.7.1 Direct Proof
Math 2903: proof if n,m even then n2 + m2 even
Discrete Math - 1.7.3 Proof by Contradiction
Discrete Math - 1.7.2 Proof by Contraposition
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Math Shower If square of n is even n is even
Discrete Math - 1.8.1 Proof by Cases
Discrete Math 1.7.2 Proof by Contraposition
Math 2200: Section 2.4 - Writing Direct Proofs
Human Calculator Solves World’s Longest Math Problem #shorts
Math Shower If square of n is even n is even
Direct Proofs (Discrete Math)
1.8.3 Proving 'If and Only If' Statements || Proofs || Discrete Math
An Intro to Proof Based Math: Direct Proofs Involving the Division of Integers
Examples of Proof by Induction (Discrete Math)
MATH 211-002- Direct Proof- 3/24
Sum of Integers Squared: Math Direct Proof Example
Комментарии
 0:04:48
0:04:48
 0:09:44
0:09:44
 0:22:09
0:22:09
![[Discrete Mathematics] Direct](https://i.ytimg.com/vi/uDJfx4bK3Jc/hqdefault.jpg) 0:06:59
0:06:59
 0:08:35
0:08:35
 0:09:00
0:09:00
 0:03:38
0:03:38
 0:07:23
0:07:23
 0:05:09
0:05:09
 0:09:40
0:09:40
 0:06:39
0:06:39
 0:05:45
0:05:45
 0:03:57
0:03:57
 0:18:46
0:18:46
 0:06:39
0:06:39
 1:09:53
1:09:53
 0:00:34
0:00:34
 0:03:59
0:03:59
 0:57:58
0:57:58
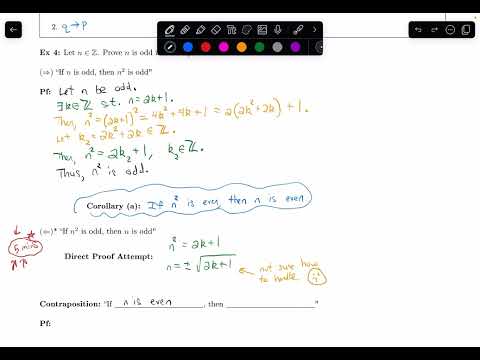 0:11:44
0:11:44
 0:32:43
0:32:43
 0:22:43
0:22:43
 0:57:52
0:57:52
 0:12:56
0:12:56