Lecture 24 - Cauchy's theorem

Показать описание

NPTEL-NOC IITM

Рекомендации по теме

Комментарии

I'm a bit confused. What is our induction hypothesis here? We showed that for the base case of |G| = 2, the statement is valid. My understanding is that our induction hypothesis should be that the statement is valid for some n and show that it implies the validity of the case |G| = n + 1. But in our induction step, we don't make any reference to |G| in that way.

bibekgautam

Isn't the first case a contradiction, he first assumed that there is no subgroup of order less than G, but in the end he proved otherwise ??

HarshKumar-chss

Construction of Gmod H is of cosets, but construction of group G is of elements originally, how you have considered that Order of Gmod H is less than order of G, let me know, and what is the guarantee that H is of G and, H is non trivial in G, it may be trivial.

tikarambhusal

Sir how to find number of all elements of order for special only non Abelian and Abelian group PLEASE REPLY JAI HIND JAI BHARAT MATA KI JAI

praveshpkofficial

So is it a thrash video?
The only Take away is
1) Prove for base case
2) Prove for some k
3) Prove k implies k+1

So The mistake he made is, he mixed up G and H and also jump of more than 1 ?

revanthkalavala

m should be prime, other wise it is obvious no ex is needed

tikarambhusal

Lecture 24 - Cauchy's theorem

Lecture 24 - Cauchy's theorem

Analysis-I | Examples of Cauchy's Theorem | Lecture- 24 | Prof. Ashwani Goyal

[Deprecated] Group Theory Lecture 6.4 Cauchy's Theorem

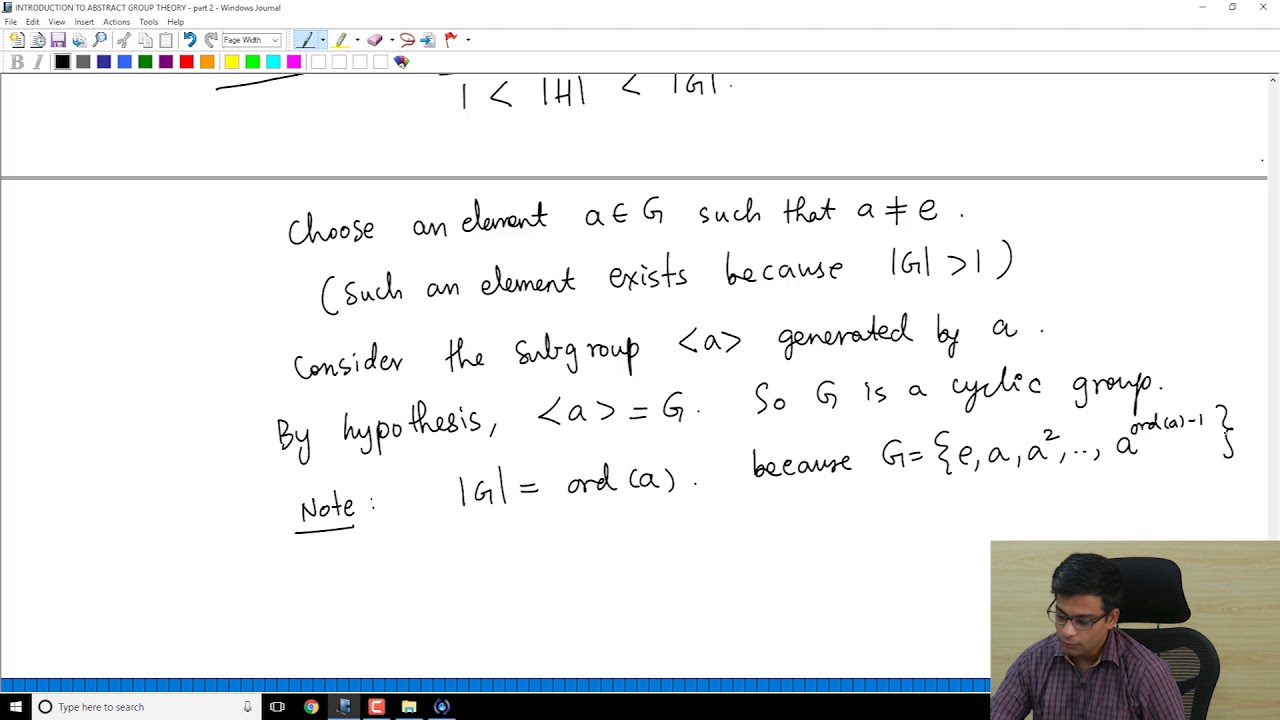
MATH 235-Abstract Algebra 1-Lecture 24- Group actions-Cauchy's Theorem And Homomorphisms

Cauchy's theorem

Visual Group Theory, Lecture 5.4: Fixed points and Cauchy's theorem

Intro Complex Analysis, Lec 24, Integration, Cauchy-Goursat Theorem, Cauchy Integral Formula

Complex Analysis: Lecture 20: Cauchy's Theorem and Integral Formula

Cauchy's Theorem Part 1

B.sc./B.A/M.sc/M.A/Groups/Sylow's 2nd Theorem#study #students #graduation #viral#youtubeshortsl

Complex integration, Cauchy and residue theorems | Essence of Complex Analysis #6

Complex Analysis | Unit 2 | Lecture 13 | Example of Cauchy's Integral Formula

Cauchy’s Theorem

Cauchy Theorem (the general case)

GT19. Cauchy's Theorem

Group Theory: 28 Cauchy's Theorem, Lagrangian Groups

Group theory 12: Cauchy's theorem

Abstract Algebra: Cauchy's Theorem and Class Equation, 10-13-17

Abstract Algebra, Lec 19B: Factor Group Applications (Cauchy's Theorem), Internal Direct Produc...

[Deprecated] Group Theory Lecture 3.10 Cauchy's Theorem for Abelian Groups

This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation

https://youtu.be/9LZwoSRAcOI Functional analysisTopic: Functional space C[a,b] is a Normed Space.

Cauchy's mean value theorem | state and prove cauchy's mean value theorem | @Rapid Educat...

48 | Cauchy theorem for Finite Abelian Group | Statement and Proof