Proof by Strong Induction [Discrete Math Class]

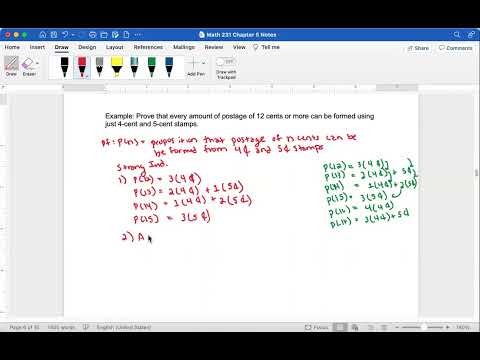
This video is not like my normal uploads. This is a supplemental video from one of my courses that I made in case students had to quarantine. In this video, we discuss the principle of strong induction: what it is for, why it works, and how to go about using the technique. We compare the technique to standard induction and then we use strong induction to prove that every positive integer has a prime factorization (we do not show uniqueness). We then show that an equilateral triangle can be tiled by n-equilateral triangles (not all congruent) for all n greater than 5. We finish by discussing a famous problem called the Chicken McNugget problem (also known as the Frobenius coin problem).

Note that this video is part of a series kept in a playlist called [Discrete Math Class]:

If you like this video, please consider subscribing to my channel and let me know in the comments if you'd like to see more like this.

This textbook for the course is the open-source textbook by Oscar Levin:

#tiling #equilateraltriangle #triangletiling #chickennuggetproblem #frobeniuscoin #induction #proofbyinduction #stronginduction #primes #primefactors #primefactorization #universalstatements #math #manim #discretemathematics

To learn more about animating with manim, check out:

_______________________________________
Background Music:

[rezhannoori]

Amazing Video. Thank you for doing this!

[oojivel]

wouldnt the prime factorization proof have infinitely many base cases?

[doomcake]

This was the video that truly clarified strong induction for me, thank you so much!

[jakobr_]

43: assume it is possible. 43 is an odd number, so we need an odd number of 9s. 43-9 = 34. The remaining 9s can be paired into 18s, which each can be instead represented by 3*6. Iff we can add 6s and 20s to get 34, 43 is possible. 6a + 20c = 34. Divide by 2. 3a + 10c = 17. Checking mod 3, c=2 or 5 or 8 etc. All of these result in sums greater than 17. Therefore a<0 and 43 is not possible.

44: given. 44=20+9+9+6
45: 45=9+9+9+9+9
46: given. 46=20+20+6
47: 47 = 44+3 = 44-6+9 = 20+9+9+9
48: 48=6+6+6+6+6+6+6+6
49: 49 = 46+3 = 46-6+9 = 20+20+9

Separate all integers greater than 49 into equivalence classes mod 6. Each equivalence class can be separately shown to be possible by normal induction, no need for strong induction here.

[supu]

Very good 👍. Learned a new thing today

[Tucan_-wjqo]

godsent thx, not gonna lie made me understand it better then sitting 1 hour at collage lecture

[pengin]

Nice! Here is another challenge using this principle for the ones interested: Show that for all n≥4, there are non-zero rational numbers a_i from i=1 to n such that the sum of the a_i² is equal to 1 while the sum of the a_i is equal to 0.

Bonus question: Prove that we don't find these a_i for n=3

Bonus bonus question: Can you show the first result while only using weak induction and not strong induction?

[teded_]

These videos should get millions of views

[mathdoctor]

Can you give me your manim source code via email?