Strong Induction and Well Ordering: Discrete Mathematics

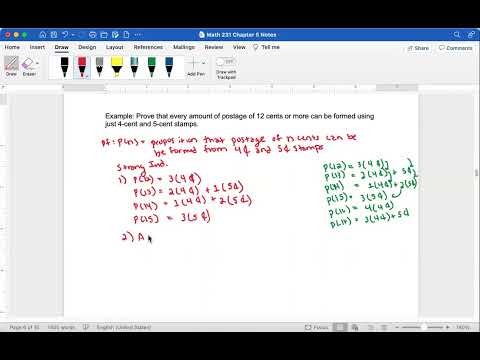
To prove this using strong induction, we do the following:
The base case. We prove that P(1) is true (or occasionally P(0) or some other P(n), depending on the problem).
The induction step. We prove that if P(1), P(2), …, P(k) are all true, then P(k+1) must also be true.
In mathematics, the well-ordering theorem, also known as Zermelo's theorem, states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. The well-ordering theorem together with Zorn's lemma are the most important mathematical statements that are equivalent to the axiom of choice (often called AC, see also Axiom of choice § Equivalents).
First, here is a proof of the well-ordering principle using induction: Let S S S be a subset of the positive integers with no least element. Clearly, 1 ∉ S , 1\notin S, 1∈/​S, since it would be the least element if it were. Let T T T be the complement of S ; S; S; so 1 ∈ T .