filmov
tv
How to solve adifferential equation with u=y/x substitution
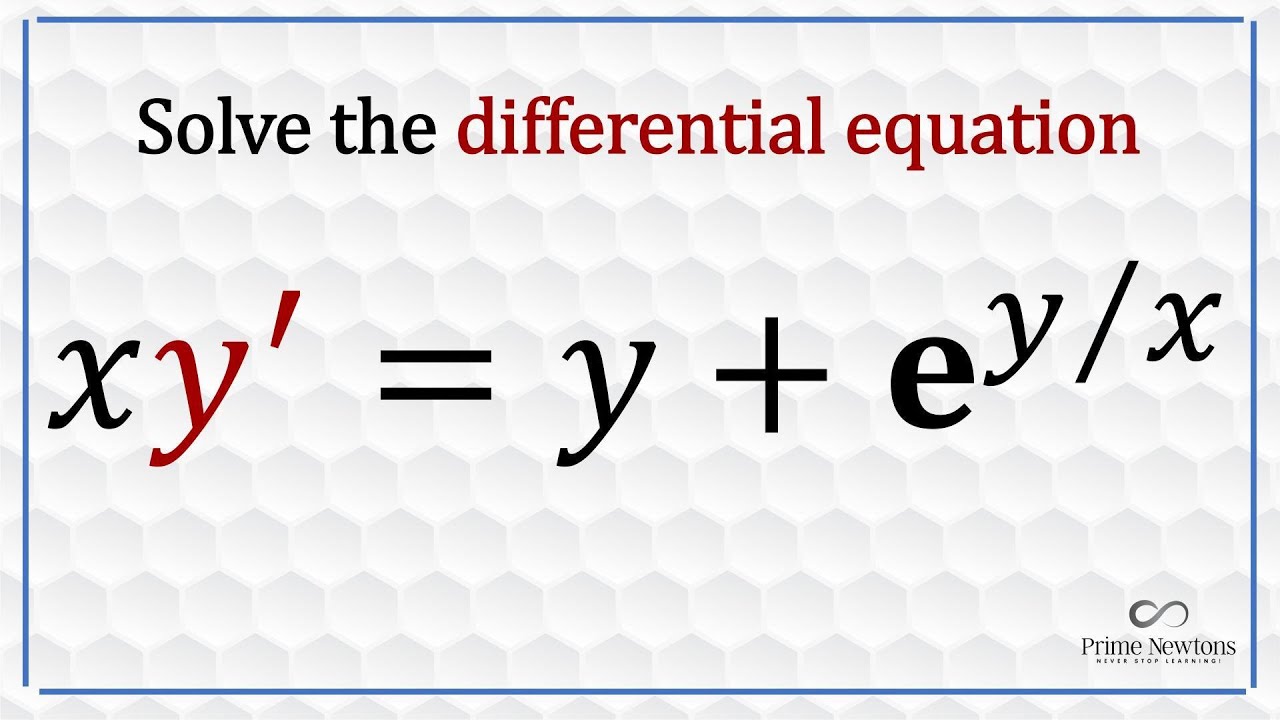
Показать описание
In this video, I showed how to solve a separable differential equation using the u = y/x substitution. Enjoy!
Solving a Differential Equation by separating the variables (2) : ExamSolu
How to determine the general solution to a differential equation
Differential equation introduction | First order differential equations | Khan Academy
Solving a differential equation using Microsoft Excel
Differential Equations - Solution of a Differential Equation
How to solve adifferential equation with u=y/x substitution
Differential equations, a tourist's guide | DE1
General Solution of a Differential Equation
Show that the differential equation |y''|+3=0 has no solution.
How to use the Annihilator Method to Solve a Differential Equation Example with y'' + 25y ...
Power Series Solution for a differential equation
How to find the particular solution of a differential equation
Solving a Differential Equation by separating the variables (1) : ExamSolutions
Topic1 tutorial solving a diff equation using op amp
Differential Equation - Introduction (4 of 15) The Solution of a Differential Equation - Ex. 2
Differential Equation - Introduction (7 of 15) Real Example of a Differential Eq - 3 Bernoulli'...
Solving Differential Equations with Power Series
How To Solve Differential Equations | By direct Integration.
Find a Differential Equation whose Solution is y = a*ln(bx)
How to solve ANY differential equation
Verifying the solution of a Differential Equation
(New Version Available) Solving Differential Equations by Separation of Variables
Ex: Solve a Differential Equation that Models the Change in a Bank Account Balance
Solve a differential equation by substitution, v=x^3+y^3, an exam question
Комментарии
 0:09:53
0:09:53
 0:02:03
0:02:03
 0:07:49
0:07:49
 0:13:40
0:13:40
 0:08:01
0:08:01
 0:08:33
0:08:33
 0:27:16
0:27:16
 0:02:31
0:02:31
 0:02:44
0:02:44
 0:12:52
0:12:52
 0:21:20
0:21:20
 0:03:28
0:03:28
 0:14:40
0:14:40
 0:08:57
0:08:57
 0:04:04
0:04:04
 0:05:50
0:05:50
 0:18:29
0:18:29
 0:07:33
0:07:33
 0:03:21
0:03:21
 0:05:05
0:05:05
 0:07:23
0:07:23
 0:06:42
0:06:42
 0:07:19
0:07:19
 0:06:04
0:06:04