filmov
tv
Does sum (n!)/(n^n) converge? - Week 3 - Lecture 4 - Sequences and Series

Показать описание
Does sum (n!)/(n^n) converge? - Week 3 - Lecture 4 - Sequences and Series
Does sum (n^5)/(4^n) converge? - Week 3 - Lecture 1 - Sequences and Series
how to use the ratio test for the series of n!/n^n
Does the Infinite Series SUM( (n + 1)^2/(n(n + 2)) ) Converge or Diverge?
Does sum 1/n converge or diverge? - Week 2 - Lecture 7 - Sequences and Series
TNT vs. RAIN OR SHINE | FULL GAME 2 SEMIS HIGHLIGHTS | PBA SEASON 49 GOVERNORS' CUP | OCT. 11, ...
Does sum 1/n^2 converge? - Week 2 - Lecture 11 - Sequences and Series
Infinite Series SUM(n/ln(n)) Does it Converge or Diverge?
Does the Series Converge Absolutely, Conditionally, or Diverge? Sum((-1)^n/n!)
Series Convergence for n!/n^n
Geometric Series | Convergence, Derivation, and Example
Choosing Which Convergence Test to Apply to 8 Series
Does sum 1/(n log n) converge? - Week 3 - Lecture 10 - Sequences and Series
Does the sum of (-1)^n converge? #shorts
If I did this in 1734 I'd be World Famous
Convergence and Divergence - Introduction to Series
Does the Series SUM(ln(n/(2n + 5)) Converge or Diverge?
Does the series SUM ( cos(n*pi)/n(3/5) ) converge conditionally, converge absolutely or diverge?
series of n^n/(n!)^2, converge or diverge?
Does Infinite Series SUM((1 + sin(n))/10^n) Converge or Diverge?
Does this series converge?
Does sum 1/n^p converge? - Week 3 - Lecture 9 - Sequences and Series
Does the Series Converge or Diverge? SUM(cos(npi)/n)
Telescoping Series
Комментарии
 0:09:06
0:09:06
 0:13:39
0:13:39
 0:08:26
0:08:26
 0:03:04
0:03:04
 0:06:40
0:06:40
 0:14:13
0:14:13
 0:09:01
0:09:01
 0:02:03
0:02:03
 0:04:17
0:04:17
 0:08:22
0:08:22
 0:06:28
0:06:28
 0:12:13
0:12:13
 0:07:40
0:07:40
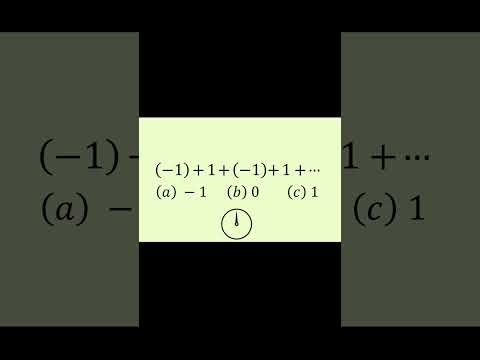 0:00:18
0:00:18
 0:03:57
0:03:57
 0:16:18
0:16:18
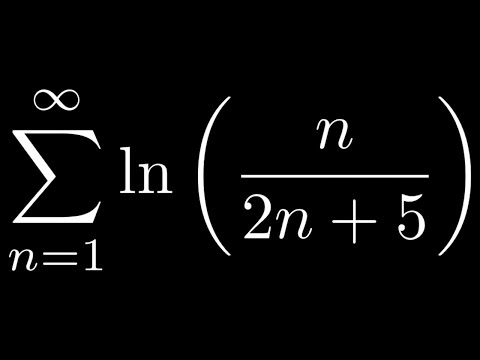 0:02:48
0:02:48
 0:01:53
0:01:53
 0:10:04
0:10:04
 0:05:06
0:05:06
 0:00:52
0:00:52
 0:08:07
0:08:07
 0:03:56
0:03:56
 0:23:39
0:23:39