filmov
tv
Does sum 1/(n log n) converge? - Week 3 - Lecture 10 - Sequences and Series
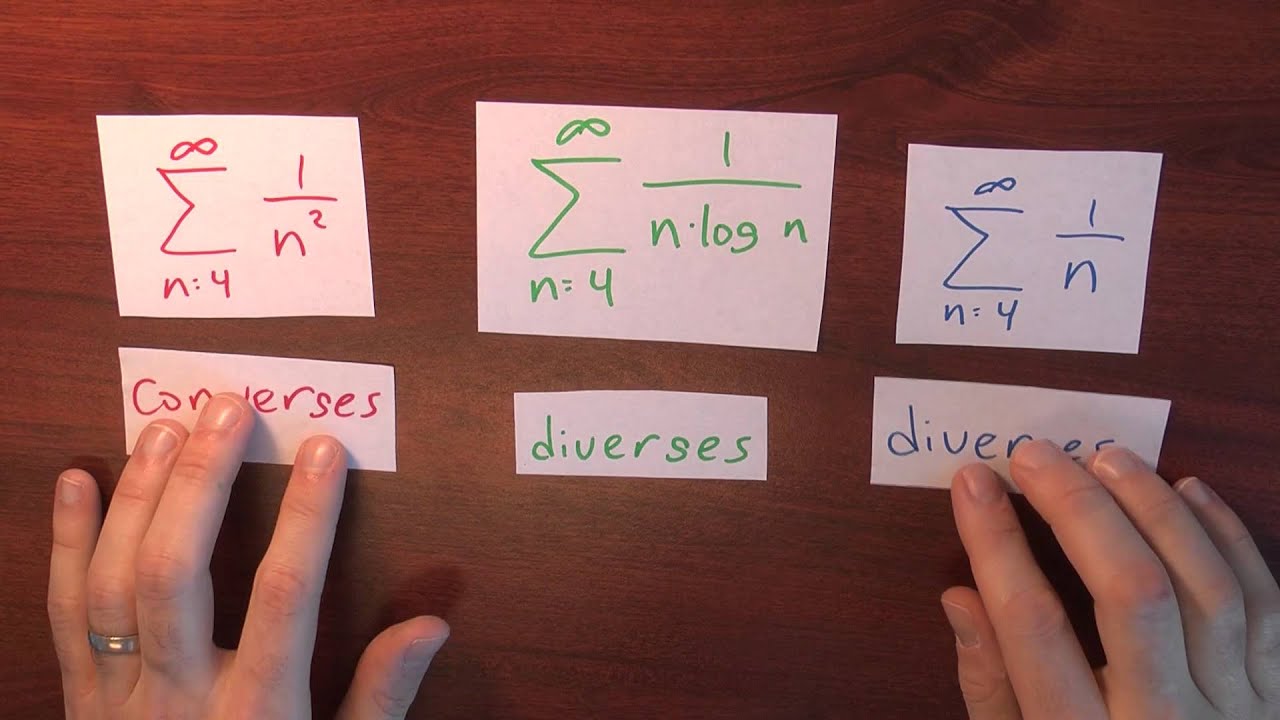
Показать описание
Does sum 1/(n log n) converge? - Week 3 - Lecture 10 - Sequences and Series
Convergence of the series (1/(log n)^(log n ))
∑ (𝑛=2) to ∞ of (𝑥−1)^𝑛/log𝑛
sum 1/(n log n)
Infinite sum 1/n*(n+1)
how to calculate the sum from 2 to infinity of 1/n.log(n)
Test the convergence of series 1/n log n
integral test sum 1 over n times log n^3
Series 1/log(n) or 1/ln(n) converges or diverges? (W/Text Explanation) |Maths |Mad Teacher
151.wk9. using cauchy's condensation test on sum 1/(n ln n)
Deeply Understanding Logarithms In Time Complexities & Their Role In Computer Science
Converges or Diverges? sum( (-1)^n n/ln(n + 1), n = 1, 2, ...)
2.1.3 Recurrence Relation (T(n)= T(n-1) + log n) #3
Sum from n=1 to infinity of ln(n)/n!
Does sum 1/n converge or diverge? - Week 2 - Lecture 7 - Sequences and Series
Direct comparison test 1/(ln(n)), including derivative proof that ln(n) is less than n. Sum 1/ln(n).
Series 1/log(n) or 1/ln(n) converges or diverges? (W/Voice Explanation) |Mad Teacher
Find the values of p for which the series converges. {1/(n(ln n)^p)}. Integral Test
100 series convergence tests (no food, no water, no stop)
Without Integral Test, Prove: Sum 1/(n ln n) Diverges
Infinite series containing 1/logn Convergent or not in 5 sec CSIR NET TRICKS| CONVERGENCE DIVERGENCE
Determine if series converges or diverges. {1/(n ln n)}. The Integral Test. [2, infinity)
Find the Interval of Convergence for the Power Series SUM((-1)^(n + 1)(x - 5)^n/(n8^n))
Relation between series 1/n and log n
Комментарии
 0:07:40
0:07:40
 0:07:30
0:07:30
 0:06:03
0:06:03
 0:14:51
0:14:51
 0:00:46
0:00:46
 0:11:47
0:11:47
 0:03:49
0:03:49
 0:05:37
0:05:37
 0:01:32
0:01:32
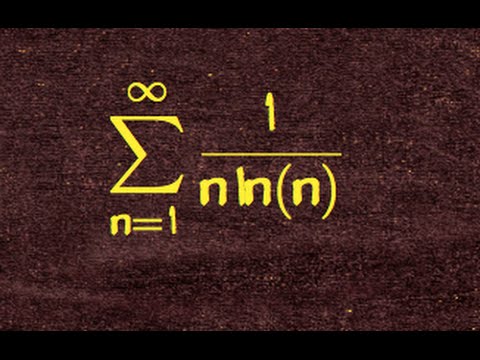 0:01:12
0:01:12
 0:10:24
0:10:24
 0:01:13
0:01:13
 0:12:25
0:12:25
 0:01:40
0:01:40
 0:06:40
0:06:40
 0:03:12
0:03:12
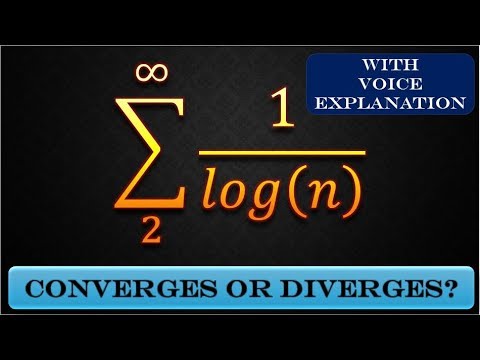 0:04:16
0:04:16
 0:09:09
0:09:09
 6:06:54
6:06:54
 0:03:21
0:03:21
 0:00:38
0:00:38
 0:04:31
0:04:31
 0:11:46
0:11:46
 0:02:46
0:02:46