Complex Numbers in Quantum Mechanics

A brief introduction to the use of complex numbers in quantum mechanics. This video is intended mostly for people who are learning quantum mechanics and have some familiarity with things like the quantum harmonic oscillator, or the hydrogen atom, but might have some confusion around what all the complex numbers are all about. I hope this video provides you with an improved sense of familiarity with the complex numbers. These things are cool. They take a bit of getting used to, but they're cool.

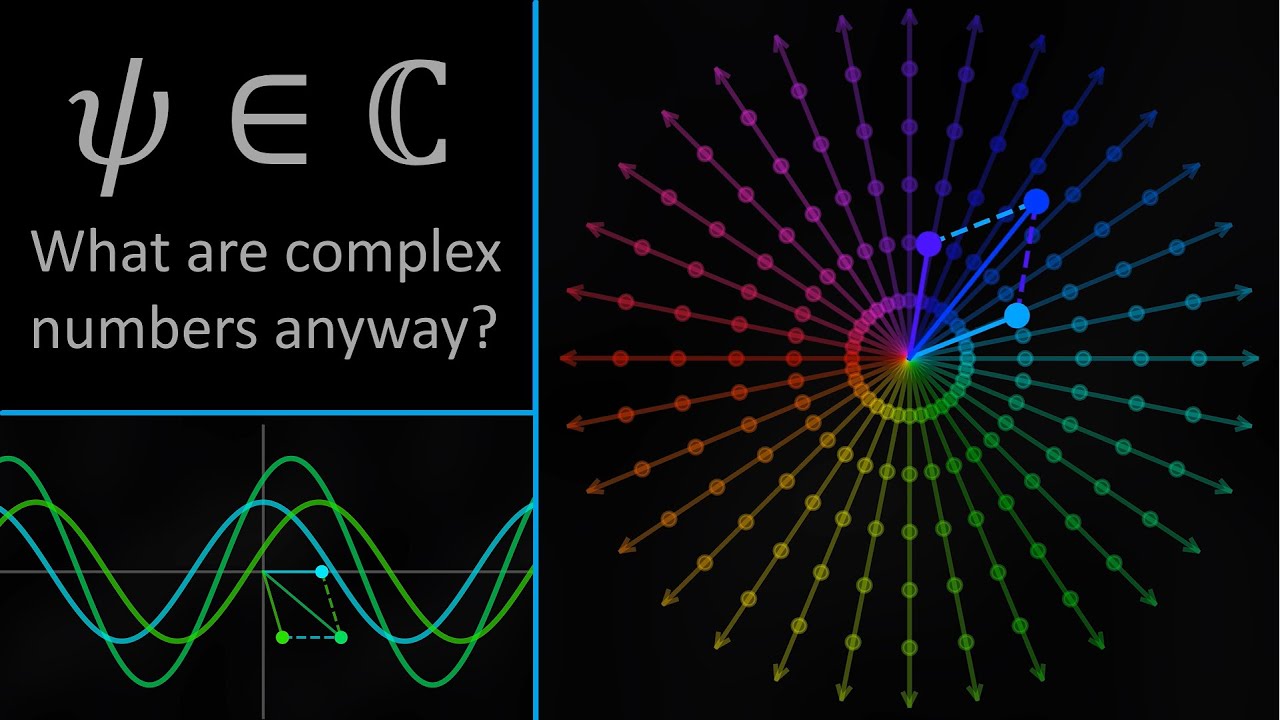
My main goal in this video is to make the complex numbers feel as natural and accessible as possible, so I emphasize the perspective that the complex phase can be thought of as a generalization of positivity and negativity, and in particular that the phase oscillates between two poles (which I half-jokingly refer to as yin and yang). This approach, though real-part-biased, is motivated by the observation that the interference of two waves of the same frequency (constructive, destructive, and everything in between) provides a natural picture for one of the things the phase of a complex number might mean. I hope that helps to demystify how complex numbers are not an entirely absurd concept, because a stumbling block for many people, myself included for a while, is that the complex numbers seem too unrealistic for human intuition to sincerely glom on to. But, as I hope this video shows, the complex numbers can be made intuitive.

It should be noted, however, that the story does not end here. Once you are familiar with the complex numbers, you should stretch your mind out again by regarding the complex numbers as equipping a model with a circular degree of freedom. In particular, you can imagine a wavefunction as a section of a fiber bundle whose base is spacetime, whose fibers are circles of mysterious origin, and whose total space is some fragment of this thing we call reality. That should keep you up at night!

I should also add that the "U(1) Symmetry implies Electromagnetism" argument may well be completely backwards. It is true that, if one takes the Dirac field with minimal coupling to the photon field, and imposes local U(1) symmetry by fiat, then all the beauty of classical electromagnetism follows. But one can easily argue that such an imposition is contrived, and more indicative of a redundancy of our model than a genuine symmetry of physics. That argument is strengthened in light of Wigner's classification, pun proudly intended, since if we take the masslessness of the photon as our starting point, then the photon can only have helicity eigenvalues of +-1, *not 0* (the photon has no rest frame), and therefore one must remove any physical contributions coming from longitudinal photon modes, since they cannot exist. This fictionalization of the longitudinal modes yields precisely the usual gauge symmetry of the four-potential (or so I am told... still need to work out for myself why this is true), and once you have the gauge symmetry of the four-potential, then your Dirac field better have local U(1) symmetry if you want to preserve minimal coupling!

Anyway, whichever direction of the argument is more true, it is still a beautiful idea that local U(1) symmetry of the Dirac field, and the usual gauge symmetry of A, and the masslessness of the photon are, for all intents and purposes, the same thing. It is still an open philosophical question as to whether all this symmetry and gauge freedom is a genuine reflection of natural symmetry, or of mere theoretical redundancy; that question boils down to whether the transformations involved are active or passive, respectively, and that quickly gets into some murky existential territory when you really think about it. Fiery debates are ongoing around these questions. But that's a topic for another time, and not one which is answerable within a YouTube video description.

Thanks for watching & reading :)

Chapters:
0:00 Introduction
1:00 Real vs. Complex Numbers
2:48 A Wavy Wave, Waving
4:33 Complex Representation of the Wave
7:48 Complex Addition, Multiplication, and Interference
12:10 Fourier Analysis & Superpositions
12:47 Examples: Harmonic Oscillator and Hydrogen
14:30 Plane Waves
16:49 Probability Density
18:07 U(1) Symmetry Implies Electromagnetism

#physics #quantum #math

[RichBehiel]

Hi everyone, thanks for checking out this video. There are a couple caveats that I put in the video description, relating to the yin-yang metaphor and the connection between local U(1) symmetry and electromagnetism, so please check those out if you are interested.

Also, I could use your advice about something. In this video, I added a bit of gray/black motion to the background, since this helps prevent YouTube's algo from adding compression artefacts to the video (moving color on a solid background would otherwise lead to a confetti-like appearance). The moving background also helps the video come to life a bit more, lets it breathe, you know? But I hope this effect does not come across as distracting or nauseating, so please let me know if in your opinion it was too much, and if I should make it more subtle or slow it down in future videos. Or, if you have another suggestion for how to add subtle motion to the background of a video without it being distracting, please let me know.

By the way, if anyone has advice for how to speak more naturally into a microphone, I would love to hear it! I feel like there's a tradeoff between annunciation and flow, like if I try to say every word properly then I sound like a robot, but if I just talk conversationally then I find that I tend to mumble a bit. Maybe I just need more practice. But if anyone has any tips or tricks or vocal exercises, please let me know.

And as always, if you have a question about anything presented in this video, just leave a comment and I, or another commenter, will get back to you soon. I highly encourage conversation around these topics, because odds are you're not the only one who has that question, so we can all learn together. That's really what this channel is all about :)

[bowfuz]

we need more mathtube and sciencetube content where the speaker talks casually and laughs more, it's hard to pin down exactly why this makes it better but i conject that the usually neglected emotional aspect of videos like these is seriously improved with humor and the occasional fumble

[nice]

I loved the motivation of complex numbers as extending the sense of "sign"/phase/direction from being discrete to continuous

[giorgosg]

Finally, a very easy and comprehensive way to explain why complex numbers are so important for wave mechanics

[ellepeterson]

WHY HAS NOONE EXPLAINED THIS TO ME LIKE THIS SO FAR this make so much sense

[aanchaallllllll]

0:03: 🧩 Quantum mechanics involves complex numbers, which initially seem confusing but are essential for understanding the subject.
3:12: 🌊 The concept of a wave and how numbers can capture its characteristics.
6:10: 📚 The imaginary and real parts of complex numbers are equally real, and representing waves as complex numbers allows for easier understanding of wave interference.
9:01: ✨ Complex numbers can be added and multiplied in the complex plane, with the product's magnitude depending on the magnitudes of the individual numbers and the phase angle depending on the sum of the phase angles.
12:05: 🔗 Complex numbers allow for the addition of waveforms in signal processing and Fourier analysis.
14:38: 🔍 Complex numbers in quantum mechanics are not about direction in physical space, but rather represent the two-dimensionality of a wave.
17:30: ✨ The amplitude squared of a complex number in quantum mechanics is often expressed as PSI star PSI, which represents the probability density relating to the wave function.
Recap by Tammy AI

[YossiSirote]

Descartes … “that and Dualism” 😂😂😂😂 … and now you are one of my favorite people ❤

[passingshots]

I struggled with complex numbers throughout all my education, I couldn't grasp the idea. The way you presented it makes complete sense because of the geometric representation. It's beautiful

[james-cucumber]

This was an incredible video. Leaving comment mostly for algorithm, but also to wish you the best of luck. This content deserves way more views

[FAS]

2 minutes in and you already blew my mind, way above my level of understanding in the later parts but somehow still coherent due to your wholistic approach, this channel is going to blow up in due time. Personally I find that I have the easiest time understanding when the purely abstract is intermingled with physical concepts and happenings and you were amazing at doing this. I think the same applies to many others as well. Thanks and I will definitely check out your other videos!

[zacwarnest-knowles]

wow I’ve just found your channel and this is crazy quality stuff and a really great intuitive perspective that helped me see the complex plane in a different light. I was a bit shocked when I saw your subscriber count I expected you to have atleast in the 10k to 100k range. You will surely blow up soon making things to this standard.

[spacecowx]

This hits wayyy different than those low quality ear grating lectures i'm accustomed to finding on youtube. Its also way different than those documentary style videos that seem to only scratch the surface. Keep up the good work

[FinalEyes]

When you said Descartes biggest mistake was calling complex numbers imaginary, "that and dualism", with a short dramatic pause, I had no choice but to pause the video, like, and subscribe. This is very helpful for understanding wtf is going on with imaginary numbers as well. Thanks.

[Marc-tmxh]

This is stuff that I've been thinking and wondering about (as a layman) for literally years. Your videos are so fantastic at giving me insight into all these ideas. I can't imagine how long it took to make all those beautiful mindblowing visualizations. Truly amazing work, thank you!

[mmer]

This is one of the most beautiful math videos i've seen. I hope you will continue doing them.

[stuartriley]

Richard thank you for the presentation and your insight on complex numbers. I have studied the works of many particle physics and few had noted the world that exists in the quantum field theory of the impact of complex numbers, and their conjugates. What we sense is not what our reality is; we cannot see it but it (complexity) is there. Thank you once again for this presentaton.

[jippijip]

Omg your visualization of a coherent state of the harmonic oscillator at 13:00 is FANTASTIC! Nice work!

[anth]

you are an artist. And you’ve found your portal into the realm of art via pure math, and it’s really stunning. I’ve never encountered anything like this. I am humbly taking the first steps of a long journey towards understanding math and physics now, and I can intuitively confirm your sentiment “it’s one of the most wholesome things you can do”. Really grateful for these videos. You are helping me find the applied science hidden in plain sight in the work I’ve devoted my life to doing (which is teach music to children)

[markawbolton]

Great timbre and natural Narration. Very pleasant and easy to follow.

[everyotherodd]

This deserves 1M+ views - the question that was answered in this video brought a lot of existential satisfaction 👏